Vecteur normal à une droite
Vecteur normal à une droite
Vecteur normal à une droite
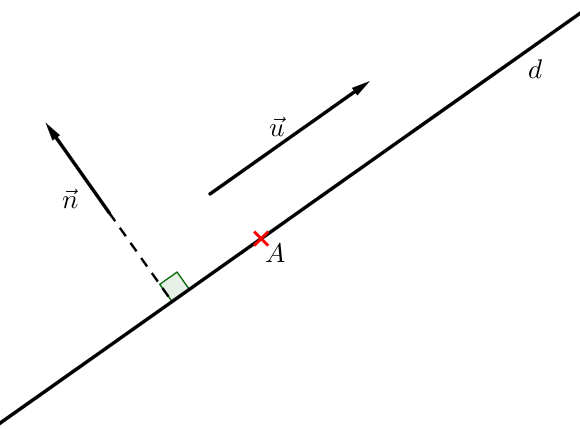
Une droite peut être définie à partir d’un de ses vecteurs directeurs. (→u sur la figure)
Elle peut également l’être à partir de l’un de ses vecteurs normaux. (→n sur la figure)
Définition :
Un vecteur normal est un vecteur orthogonal à tout vecteur directeur de la droite.
Tout vecteur colinéaire à un vecteur normal est normal à la droite.
Soient M un point quelconque de la droite (d), A un point appartenant à la droite.
Si →n est un vecteur normal à cette droite, alors :
→AM.→n=0.
Vecteur normal et équation cartésienne de droite
On se place dans un repère.
On peut donc écrire les coordonnées des différents éléments précédents :
→n(ab), M(x;y) et A(xA;yA).
L’équation →AM.→n=0 permet de trouver une équation cartésienne de la droite (d) de la forme
(d):ax+by+c=0, avec c=−axA–byA.
Cette équation cartésienne n’est pas unique à l’inverse de l’équation réduite (y=ax+b) qui est unique.
Exemple :
On considère l’équation cartésienne suivante 4x+2y–6=0.
D’après le cours, on peut lire les coordonnées d’un vecteur normal →n à partir de cette équation : ainsi
→n(42).
Un coefficient directeur →u d’une droite d’équation réduite y=ax+b est →u(1a).
Ainsi, un coefficient directeur de la droite d’équation y=−2x+3 est →u(1−2).
