Transformation de $MA^2+MB^2$

Transformation de ${MA}^2 + {MB}^2$. Formule de la médiane

Transformation de ${MA}^2 + {MB}^2$ à l’aide du milieu de $[AB]$ – Formule de la médiane

I) Théorème de la médiane : transformation de l’expression ${MA}^2 + {MB}^2$

Propriété : 

Soient deux points $A$ et $B$ et $I$ milieu de $[AB]$,

Pour tout point $M$, on a :

${MA}^2 + {MB}^2 = 2{MI}^2 + \dfrac{{AB}^2}{2}$

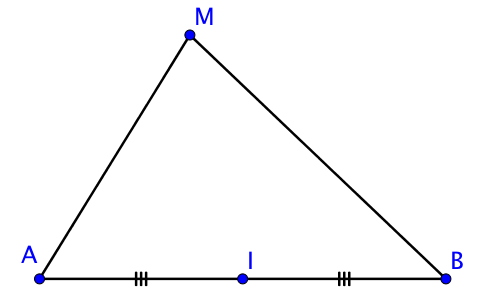
Cette formule s’appelle la formule de la médiane car elle fait intervenir $MI$ qui est la longueur de la médiane relative à $[AB]$. 

Rappels :

Le produit scalaire $\overrightarrow{MA} . \overrightarrow{MA}$ peut être calculé de différentes manières.

Il peut être calculé en considérant le produit de la norme de $\overrightarrow{MA}$ par la norme du projeté orthogonal de $\overrightarrow{MA}$ sur lui même, à savoir lui même.

Autrement dit,  $\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA = {MA}^2$, où $MA = \| \overrightarrow{MA} \|$.

On peut aussi utiliser la formule faisant intervenir le cosinus de l’angle orienté entre les deux vecteurs :

$\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA \times \cos(\overrightarrow{MA};\overrightarrow{MA})$. 

Or $(\overrightarrow{MA};\overrightarrow{MA}) = 0$ et comme $\cos(0) = 1$ alors

$\overrightarrow{MA} . \overrightarrow{MA} = MA \times MA = {MA}^2$

On a ainsi l’égalité suivante :

$\overrightarrow{MA}^2 = \overrightarrow{MA} . \overrightarrow{MA} = {MA}^2$

Preuve de la propriété :

Soient deux points $A$ et $B$ et $I$ milieu de $[AB]$,

Soit $M$ un point quelconque du plan,

${MA}^2 + {MB}^2 = \overrightarrow{MA}^2 + \overrightarrow{MB}^2$

${MA}^2 + {MB}^2=\left (\overrightarrow{MI} + \overrightarrow{IA} \right)^2 + \left(\overrightarrow{MI} + \overrightarrow{IB}\right)^2$

${MA}^2 + {MB}^2=({MI}^2 + 2 \overrightarrow{MI}.\overrightarrow{IA} +{IA}^2) + ({MI}^2 + 2 \overrightarrow{MI}.\overrightarrow{IB} +{IB}^2)$.

On regroupe alors et factorise les termes communs :

${MA}^2 + {MB}^2 =  2 \overrightarrow{MI}^2  + 2\overrightarrow{MI}.(\overrightarrow{IA} + \overrightarrow{IB} ) + \overrightarrow{IA}^2 + \overrightarrow{IB}^2$.

Comme $I$ est le milieu de $[AB]$, $\overrightarrow{IA} + \overrightarrow{IB} = \overrightarrow{0}$. 

Ainsi , ${MA}^2 + {MB}^2 = 2 {MI}^2 + {IA}^2 + {IB}^2$.

Or, $IA  = IB = \dfrac{AB}{2}$ donc finalement :

${MA}^2 + {MB}^2 = 2 {MI}^2 + \left ( \dfrac{AB}{2} \right )^2 + \left ( \dfrac{AB}{2} \right )^2 =  2 {MI}^2 + \dfrac{{AB}^2}{2}$

II) Applications

Exemple 1 :

Soit $AMB$ un triangle et $I$ milieu de $[AB]$,

Calculer la longueur $MI$ sachant que $MA = 7$ cm, $MB = 5$ cm et $AB = 8$ cm. 

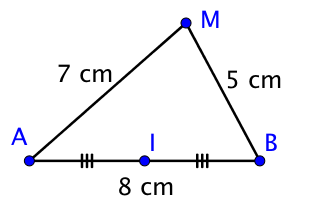
On applique la formule de la propriété précédente :

${MA}^2 + {MB}^2 = 2{MI}^2 + \dfrac{{AB}^2}{2}$.

On isole alors ${MI}^2$ : 

$2{MI}^2 = {MA}^2 + {MB}^2 – \dfrac{{AB}^2}{2}$. 

Puis on remplace par les valeurs numériques :

$2{MI}^2 = 7^2 + 5^2 – \dfrac{8^2}{2} = 49 + 25 – 32 = 42$.

Ainsi ${MI}^2 = 21$, enfin $MI = \sqrt{21}$ car $MI$ est une longueur donc est positive. 

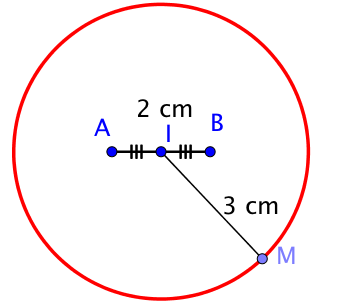
Exemple 2 : Un problème de lieu

Soient $A$ et $B$ deux points tels que $AB = 2$ cm.

On cherche à déterminer l’ensemble des points $M$ tels que ${MA}^2 + {MB}^2 = 20$.

Pour résoudre cet exercice, on utilise à nouveau la formule de la médiane.

Soit $M$ un point quelconque du plan,

${MA}^2 + {MB}^2 = 20 \iff  2{MI}^2 + \dfrac{{AB}^2}{2} = 20$

$\iff  2{MI}^2 + \dfrac{{2}^2}{2} = 20$

$\iff 2{MI}^2 + 2 = 20$

$\iff   2{MI}^2 = 18\iff  {MI}^2 = 9   \iff MI = 3$ 

L’ensemble des points $M$ tels que ${MA}^2 + {MB}^2 = 20$ sont l’ensemble des points tels que $MI = 3$, c’est à dire les points $M$ situés à une distance de 3 centimètres de $I$, ou encore l’ensemble des points appartenant au cercle de centre $I$ et de rayon $3$ cm.