Théorème de Pythagore et sa réciproque

Revenir au chapitre

Crée ton compte

1
Théorème de Pythagore
2
Réciproque du théorème de Pythagore

Théorème de Pythagore

Si $ABC$ est un triangle rectangle en $A$ , alors ${AB}^2 + {AC}^2 = {BC}^2$

Ou encore :

la somme des carrés des deux petits côtés est égale au carré de l’hypoténuse.

Cette relation permet, en connaissant la longueur de deux côtés, de trouver la longueur du dernier côté.

Exemple :

Soit $OMP$ un triangle rectangle en $O$ , tel que $OM = 5$ et $MP = 13$ .

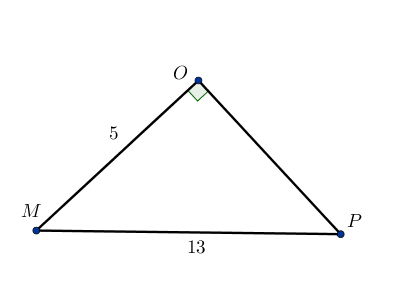
D’après le théorème de Pythagore appliqué au triangle rectangle $OMP$ rectangle en $O$ ,

${OM}^2 + {OP}^2 = {MP}^2$

$5^2 + {OP}^2 = {13}^2$

$25 + {OP}^2 = 169$

${OP}^2 = 169 – 25$

${OP}^2 = 144$

$OP = \sqrt{144}$

$OP = 12$

Réciproque du théorème de Pythagore

Soit $ABC$ un triangle,

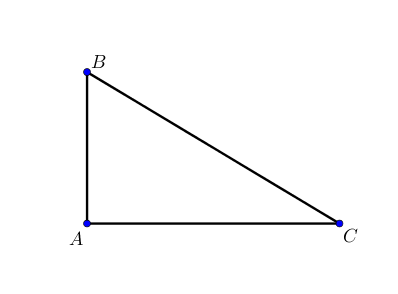
si ${AB}^2 + {AC}^2 = {BC}^2$ , alors $ABC$ est un triangle rectangle en $A$

ou encore

si la somme des carrés des deux petits côtés est égale au carré du troisième alors le triangle est rectangle et le troisième côté est l’hypoténuse.

Ce théorème permet de prouver qu’un triangle est rectangle en connaissant la valeur de ses côtés.

Exemple :

Soit un triangle $RST$ tel que $RT = 1,2$ $TS = 1,6$ $RS = 2$ .

Si l’énoncé ne fournit pas de schéma, il est utile d’en faire un à main levée qui respecte les proportions (le plus grand côté sur le schéma correspond au plus grand côté du triangle $RST$ ).

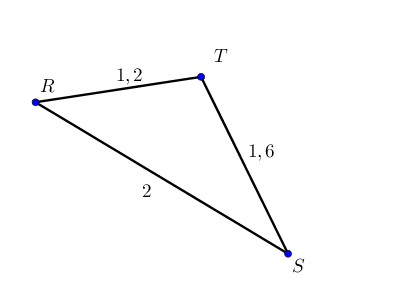
Si ce triangle est rectangle, alors son hypoténuse est $RS$ car c’est le plus grand côté.

On calcule alors ${RS}^2$ que l’on compare à ${RT}^2 + {TS}^2$ .

Ainsi, ${RS}^2 = 2^2 = 4$ .

De même, ${RT}^2 + {TS}^2 = {1,2}^2 + {1,4}^2 = 1,44 + 2,56 = 4$ .

Donc ${RS}^2 = {RT}^2 + {TS}^2$ .

D’après la réciproque du théorème de Pythagore, le triangle $RST$ est rectangle en $T$ .