Tangente à une courbe en un point

Tangente à une courbe en un point

Tangente à une courbe en un point

Soit $f$ une fonction définie sur $I$ et $a \in I$, 

La limite du taux d’accroissement en un point $a$ lorsqu’elle existe donne le nombre dérivée de la fonction $f$ en $a$ :

$\lim \limits_{h \to 0} \dfrac{f(a+h) – f(a)}{h} = f'(a)$.

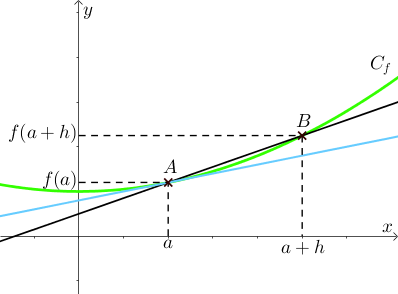
L’équation de la droite tangente à la courbe au point $a$ est

$T_a : y = f'(a)(x – a) + f(a)$.

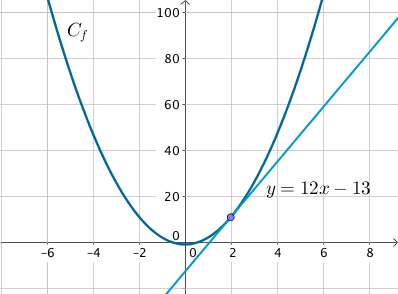
Exemple :  

Soit $f(x) = 3x^2 -1$, on cherche l’équation de la tangente à la courbe au point d’abscisse $x =2$. 

On calcule $f(2) = 11$.

On calcule ensuite la dérivée $f'(x) = 3 \times 2x = 6x$.

Ainsi, $f'(2) = 12$.

Graphiquement le nombre dérivé de la fonction en un point $a$ est le coefficient directeur de la tangente au point d’abscisse $a$. 

Enfin, 

$T_2 : y = f'(2)(x – 2) + f(2)$

$y = 12(x – 2) + 11$

$y = 12x – 13$