Suites géométriques

Suites géométriques - Définition

Suites géométriques

1) Définition 

Une suite géométrique est une suite pour laquelle chaque terme permet de déduire le suivant en étant multiplié par une constante $q$, la raison. 

Une suite géométrique est ainsi définie par

$\left \{ \begin{array}{l} u_{n + 1} = u_n \times q \\ u_0 \\ \end{array} \right.$ où $q$ est la raison ($q \in \mathbb{R}$) et $u_0$ est le premier terme de la suite. 

Considérons une suite géométrique de raison $2$ de premier terme 5 qui s’écrit alors :

$\left \{ \begin{array}{l} u_{n + 1} = u_n \times 2 \\ u_0=5 \\ \end{array} \right.$

Les premiers termes de la suite sont donc :

$u_1 = u_0 \times 2 = 5 \times 2 = 10$   et   

$u_2 = u_1 \times 2 = 10 \times 2 = 20$. 

Propriété : expression de $u_n$ en fonction de $n$.

Néanmoins la définition d’une suite géométrique nécessite pour calculer un terme de la suite d’avoir au préalable calculé tous les termes précédents. 

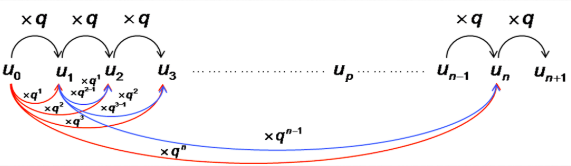
Pour passer de $u_0$ à $u_n$, on remarque qu’il a fallu multiplier $u_0$ $n$ fois par $q$ :

Ainsi : $u_n = u_0 \times q^n$ pour tout $n \in \mathbb{N}$.

La formule plus générale permet de calculer tous les termes si l’on ne connait pas le premier terme mais le $p^{\text{ème}}$ :

Pour tous $n, \ p \in \mathbb{N}, u_n = u_p \times q^{(n – p)}$.

En reprenant l’exemple précédent, on trouve $u_4 = u_0 \times q^4 = 5 \times 2^4 = 80$