Somme des angles d'un triangle
Somme des angles d'un triangle
Somme des angles d’un triangle
Propriété
La somme des mesures des angles d’un triangle vaut 180°.
Exemple :
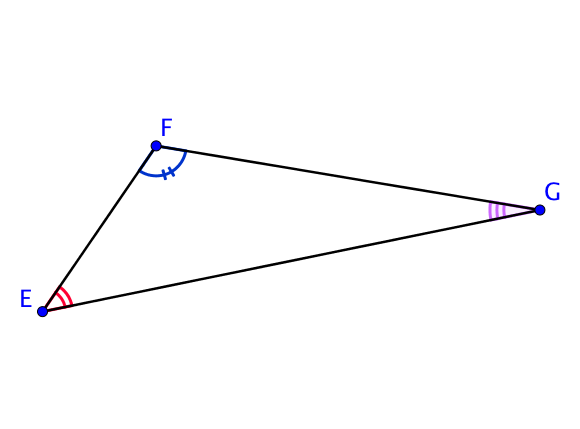
On se place dans le triangle EFG.
D’après la propriété précédente, on a l’égalité suivante :
^EFG+^FGE+^GEF=180 °.
Ainsi, en connaissant la mesure de deux angles, il est possible d’en déduire la valeur du dernier.
Exemple :
Supposons que ^EFG=100° et ^GEF=50°
Alors
^EFG+^FGE+^GEF=100+50+^FGE
^EFG+^FGE+^GEF=150+^FGE
On sait aussi que :
^EFG+^FGE+^GEF=180.
Ainsi,
^FGE=180–150=30°.
Cas particuliers :
1) Le triangle rectangle
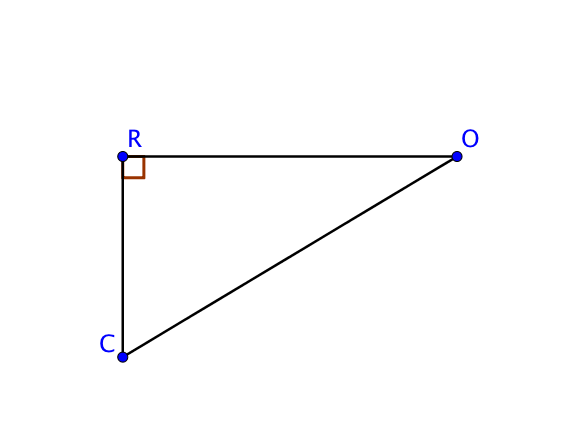
On sait que l’angle droit mesure 90°, donc ^ORC=90°.
Ainsi,
^ROC+^OCR=180–90=90°.
Deux angles dont la somme des mesures vaut 90° s’appellent des angles complémentaires.
Les deux angles aigus ^ROC et ^OCR sont donc des angles complémentaires.
2) Le triangle isocèle
Par définition, un triangle isocèle est un triangle ayant deux côtés de même longueur.
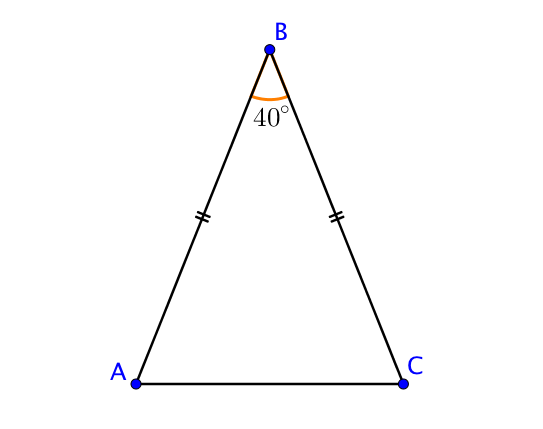
ABC est un triangle isocèle en B, ce qui signifie que BA=BC mais aussi que les deux angles à la base sont de même mesure.
Si on sait que ^ABC=40°, on peut en déduire la valeur des autres angles.
En effet,
^BCA+^CAB=180–40
^BCA+^CAB=140°.
Or ^BCA=^CAB, donc il mesure chacun la moitié de 140.
Ainsi,
^BCA=^CAB=70°
3) Le triangle équilatéral
Un triangle équilatéral est un triangle ayant ses trois côtés de même longueur.
En outre, les angles d’un triangle équilatéral ont même mesure.
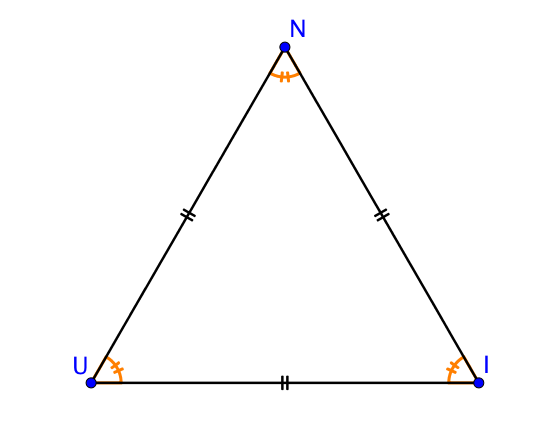
UNI est un triangle équilatéral.
Chaque angle est égal et la somme vaut 180°, ce qui signifie que chaque angle mesure le tiers de 180°, c’est à dire 60°.
