Résolution d’équations trigonométriques

Résolution d'équations trigonométriques

Résolution d’équations trigonométriques

Soit $x$ un réel appartenant au cercle trigonométrique. 

On associe à ce réel son cosinus et son sinus. 

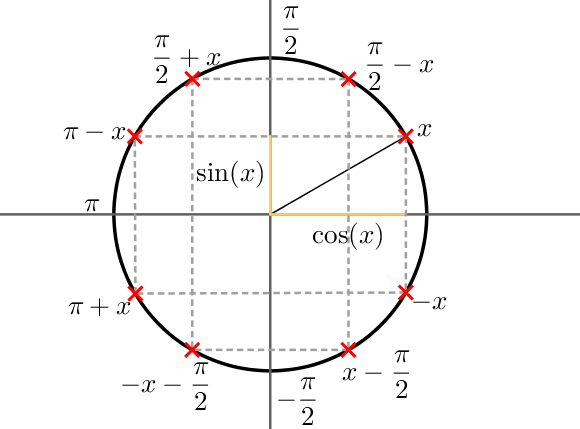
A partir du schéma, on remarque que $\cos \left ( \dfrac{\pi}{2} – x \right ) = \sin(x)$ et  $\sin \left ( \dfrac{\pi}{2} – x \right ) = \cos(x)$.

On peut également écrire que $\cos \left ( \dfrac{\pi}{2} + x \right ) = – \sin(x)$ et $\sin \left ( \pi – x \right ) =  \sin(x)$.

On peut également retrouver ces formules à partir des formules d’addition. 

Les équations trigonométriques

Il s’agit dans un premier temps de résoudre $\cos(x) = \cos(y)$.

Or deux angles ont le même cosinus si et seulement si ils sont égaux ou opposés.

Ainsi,  $\cos(x) = \cos(y) \iff \left \{ \begin{array}{c} x = y + 2k \pi \\  x = – y + 2k \pi \end{array} \right. k \in \mathbb{Z}$

L’équation $\sin(x) = \sin(y)$ est équivalente à$\left \{ \begin{array}{c} x = y + 2k \pi \\  x = \pi – y + 2k \pi \end{array} \right. k \in \mathbb{Z}$