Produit scalaire, propriétés

Produit scalaire, propriétés

Produit scalaire, propriétés

Définitions

Il existe plusieurs façons de définir le produit scalaire. 

1) Avec les coordonnées 

Soient $\overrightarrow{u} \left ( \begin{array}{c} x \\ y \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} x’ \\ y’ \\ \end{array} \right )$ deux vecteurs,
le produit scalaire de $\overrightarrow{u}$ scalaire $\overrightarrow{v}$ vaut $\overrightarrow{u} . \overrightarrow{v} = {xx}’ + {yy}’$. 

Exemple :

si $\overrightarrow{u} \left ( \begin{array}{c} 2 \\ 3 \\ \end{array} \right )$ et $\overrightarrow{v} \left ( \begin{array}{c} 4 \\ -1 \\ \end{array} \right )$ alors $\overrightarrow{u} . \overrightarrow{v} = 2 \times 4 + 3 \times (-1) = 5$. 

Le résultat d’un produit scalaire n’a pas d’unité. 

On prêtera une attention particulière au fait d’utiliser un point pour signifier le produit scalaire entre deux vecteurs. 

A partir des coordonnées, il est possible de calculer la norme d’un vecteur, c’est à dire sa longueur : $\| \overrightarrow{u} \| = \sqrt{x^2 + y^2}$.  

2) Avec l’angle

On dispose ici de la norme de $\overrightarrow{u}$ notée $\| \overrightarrow{u} \|$ qui correspond à la longueur du vecteur et de la norme de $\overrightarrow{v}$ notée $\| \overrightarrow{v} \|$ ainsi que de l’angle orienté $(\overrightarrow{u}, \overrightarrow{v})$. 

Dans ce cas, le produit scalaire vaut : $\overrightarrow{u} . \overrightarrow{v} = \| \overrightarrow{u} \| \times \| \overrightarrow{v} \| \times \cos(\overrightarrow{u}, \overrightarrow{v})$. 

Cela permet aussi d’exprimer le cosinus de l’angle : $\cos(\overrightarrow{u}, \overrightarrow{v}) = \dfrac{\overrightarrow{u} . \overrightarrow{v}}{ \| \overrightarrow{u} \| \times \| \overrightarrow{v} \|}$.

Dans certains exercices, on utilisera les coordonnées pour calculer le produit scalaire et la normes des vecteurs et on en déduire à partir de la formule précédente le cosinus de l’angle. 

Exemple : Si $\| \overrightarrow{u} \| = 2$, $\| \overrightarrow{v} \| = 3$ et $(\overrightarrow{u}, \overrightarrow{v}) = \dfrac{\pi}{3} (2\pi)$, alors $\overrightarrow{u} . \overrightarrow{v} = 2 \times 3 \times \cos \left ( \dfrac{\pi}{3} \right )  = 3$. 

Ainsi, cette formule s’utilise dès lors que l’on connait un angle. 

3) Avec le projeté orthogonal

Le projeté orthogonal d’un point sur une droite $(d)$ correspond à l’intersection de la droite perpendiculaire à la droite $(d)$ passant par ce point avec la droite $(d)$.

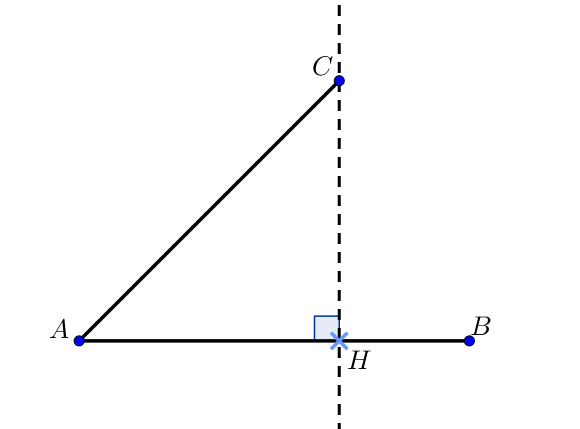
Soit $H$ le projeté orthogonal de $C$ sur $(AB)$,

alors $\overrightarrow{AB}.\overrightarrow{AC} = \overrightarrow{AB}.\overrightarrow{AH}$.

Or les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.

Ainsi l’angle les séparant vaut soit 0 soit $\pi$ selon que les vecteurs sont dans le même sens ou dans le sens contraire. 

Ainsi, $\overrightarrow{AB}.\overrightarrow{AH}$ sera égal au produit des normes multiplié par $\pm 1$ selon le sens des vecteurs. 

4) Autres formules

Il existe deux autres formules moins utilisées permettant de calculer le produit scalaire de $\overrightarrow{u}$ scalaire $\overrightarrow{v}$:
$\overrightarrow{u}. \overrightarrow{v} = \dfrac{1}{2} \left ( \| \overrightarrow{u + v} \|^2 – \| \overrightarrow{u} \|^2 – \| \overrightarrow{v} \|^2 \right )$

$\overrightarrow{u}. \overrightarrow{v} = \dfrac{1}{2} \left (\| \overrightarrow{u} \|^2 + \| \overrightarrow{v} \|^2 -\| \overrightarrow{u – v} \|^2 \right )$

Propriété

Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul (avec $\overrightarrow{u} \neq \overrightarrow{0}$ et $\overrightarrow{v} \neq \overrightarrow{0}$). 

C’est à dire si $\overrightarrow{u}. \overrightarrow{v}=0$