Modélisation : croissance et décroissance exponentielle

Modélisation : croissance et décroissance exponentielle

Modélisation : croissance et décroissance exponentielle

On se propose ici d’illustrer différentes utilisations de la fonction exponentielle. 

Exemple 1 : Placement d’un Capital

On dépose à la banque à l’instant $t = 0$ un capital de $C_0 = 12\,000 €$.

L’évolution du capital est modélisé pour tout $t \in \mathbb{R}$ par  : $\left \{ \begin{array}   C(t) = C_0 e^{pt} \\ p \text{ taux annuel} \\ t \text{ nombre d’années} \end{array} \right.$

On suppose ici que $p = 1 \%$. 

Ainsi, pour tout réel $t$, $C(t) =12\, 000 e^{0,01 t}$. 

Or $C$ est dérivable sur $\mathbb{R}$ et $C'(t) = 12\, 000 \times 0,01 e^{0,01 t} = 120 {0,01 t}$.

Ainsi, $C'(t) > 0$, la fonction $C$ est donc strictement croissante sur $\mathbb{R}$.

Enfin, on a $C(1) = 12\,121 €$ et  $C(2) = 12\,242 €$

Exemple 2 : l’offre et la demande 

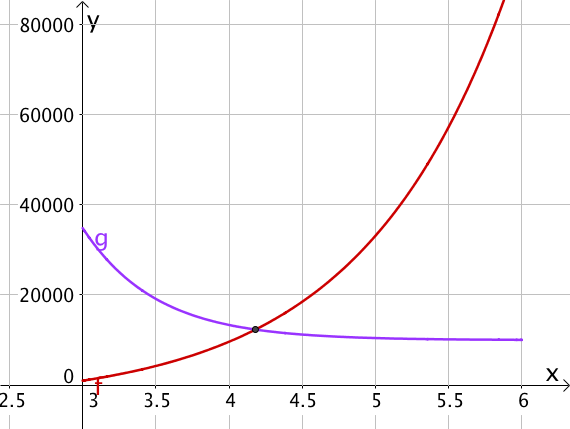
On représente l’offre par la fonction définie pour $t \in [3; 6]$ qui représente le prix unitaire par $f(t) = 250e^t – 4000$ qui est une fonction croissante et la demande par la fonction définie pour $t \in [3; 6]$ par $g(t) = 10^7 e^{-2t} + 10 000$ qui est une fonction décroissante. 

On peut trouver le prix d’équilibre correspondant à l’abscisse du point d’intersection des deux courbes. 

Graphiquement on trouve $t \approx 4,2 €$. 

On peut aussi chercher à la calculatrice une valeur de $t$ vérifiant $f(t)=g(t)$, c’est dire vérifiant :

$250e^t – 4000=10^7 e^{-2t} + 10 000$

$\iff 250e^t-10^7 e^{-2t} – 14000=0$

Exemple 3 : Loi de désintégration 

On dispose d’une quantité initiale $N_0$ d’éléments radioactifs qui se désintègrent en suivant la loi définie pour tout réel $t$ positif par : 

$N(t) = N_0 e^{-\lambda t}$; avec $\lambda = 0,121$ pour l’élément Carbone 14 et $t$le temps en années.

On peut déterminer avec ce type de modèle la quantité de matière restante pour toute valeur de $t$ souhaitée.