Angle orienté et lignes trigonométriques
Angle orienté et lignes trigonométriques
Angle orienté et lignes trigonométriques
Le cercle trigonométrique est un cercle de centre O et de rayon 1.
On place le point M sur le cercle défini par un réel en radian, qui correspond à un angle de π3 ou encore de 60° par rapport à l’axe des abscisses.
Cependant, le point M correspond à d’autres réels. En effet, si on tourne d’un tour autour du cercle, on retrouve le point M.
Comme le cercle a un rayon de 1, faire un tour signifie rajouter 2π.
Ainsi le point M est aussi défini comme le réel π3+2π=7π3.
Donc le point M correspond à une infinité de point de la forme π3+2kπ avec k∈Z ou encore π3(modulo 2π).
Le cosinus correspond à l’abscisse du point M alors que le sinus correspond à son ordonnée.
Application :
On cherche à trouver l’angle entre deux vecteurs →u et →v.
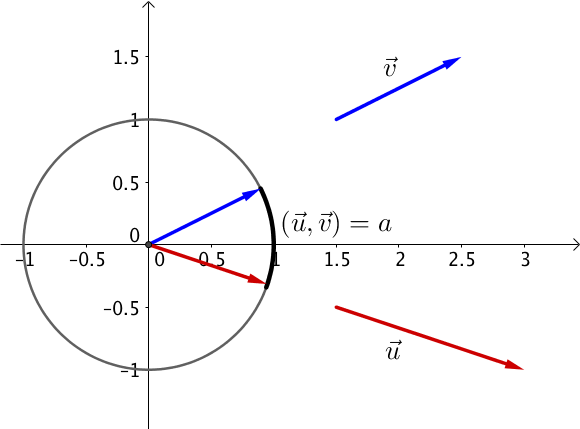
Pour se faire, il faut dans un premier temps les reporter sur le cercle trigonométrique en gardant leur sens et leur direction. L’angle entre les deux vecteurs correspond alors à la longueur de l’arc de cercle compris entre ces deux vecteurs.
On notera ainsi (→u,→v)=a+2kπ,k∈Z.
La mesure principale d’un angle est l’unique valeur de l’angle comprise entre ]−π;π].
Formules d'additions
Résolution d'équations trigonométriques
Résolution d’équations trigonométriques
Soit x un réel appartenant au cercle trigonométrique.
On associe à ce réel son cosinus et son sinus.
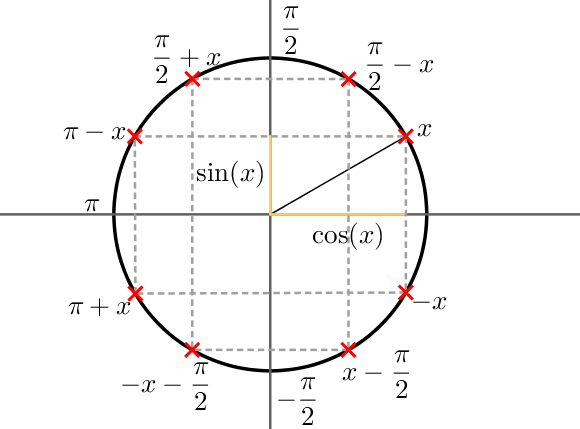
A partir du schéma, on remarque que cos(π2–x)=sin(x) et sin(π2–x)=cos(x).
On peut également écrire que cos(π2+x)=–sin(x) et sin(π–x)=sin(x).
On peut également retrouver ces formules à partir des formules d’addition.
Les équations trigonométriques
Il s’agit dans un premier temps de résoudre cos(x)=cos(y).
Or deux angles ont le même cosinus si et seulement si ils sont égaux ou opposés.
Ainsi, cos(x)=cos(y)⟺{x=y+2kπx=–y+2kπk∈Z
L’équation sin(x)=sin(y) est équivalente à{x=y+2kπx=π–y+2kπk∈Z
