Définition du logarithme népérien
Définition du logarithme népérien
Définition
La fonction logarithme népérien est l’unique fonction f, définie et dérivable sur ]0;+∞[ qui vérifie f(1)=0f′(x)=1x
On remarquera ici que l’on définit la fonction f à partir de sa dérivée.
En outre, on peut noter que l’on ne connaissait jusqu’à présent pas de fonction dont la dérivée valait 1x.
En supposant que le cours portant sur les intégrales a déjà été étudié, on peut alors définir la fonction logarithme népérien, que l’on note ln comme étant la primitive de x↦1x sur ]0;+∞[ et qui s’annule en 1.
Ainsi, pour tout réel x>0,
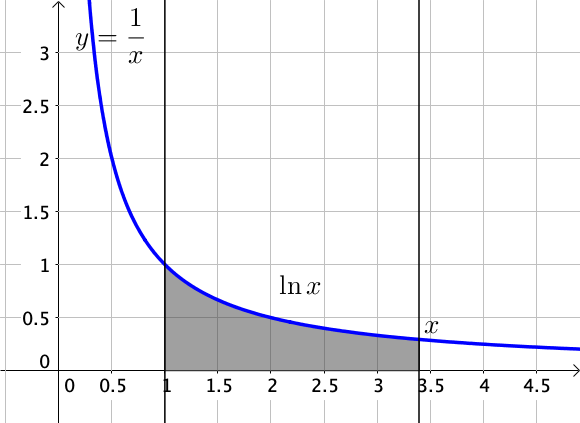
lnx=∫x11tdt
On notera que lorsque x=1, ln1=∫111tdt=0.
Graphiquement, la fonction lnx correspond à l’aire sous la courbe de la fonction inverse, comprise entre les droites verticales d’abscisse 1 et x.
Propriétés analytiques
Propriétés analytiques
La fonction ln est définie et dérivable sur ]0;+∞[.
Pour tout réel x>0,(lnx)′=1x.
La fonction ln est continue et strictement croissante sur ]0;+∞[.
D’autre part,
ln(1)=0
ln(e)=1
limx→+∞lnx=+∞
limx→0x>0lnx=−∞
Variations et représentation graphique


Théorème des croissances comparées
Théoréme des croissances comparées
Pour n appartenant à N :
1. limx→0x>0xlnx=0 et limx→0x>0xnlnx=0.
2. limx→+∞lnxx=0 et limx→+∞lnxxn=0.
Exemple
Calculer limx→+∞x3−lnx.
étape 1 : On repére une forme indéterminée du type ∞−∞ et on factorise par x3.
limx→+∞x3−lnx=limx→+∞x3(1−lnxx3)
étape 2 : On utilise le théoréme des croissances comparées pour lever l’indétermination.
On sait que: limx→+∞lnxx3=0.
Ainsi, le terme dans la parenthése tend vers 1 et par produit de limites, on obtient :
limx→+∞x3(1−lnxx3)=+∞
Nombre dérivé en 1
A savoir : limh→0ln(1+h)h=1
Preuve :
On calcule limh→0ln(1+h)h.
étape 1 : On réécrit la limite de manière à faire apparaître ln1 au numérateur et 1 au dénominateur.
On vérifie aisément que h=1+h−1.
limh→0ln(1+h)h=limh→0ln(1+h)−ln11+h−1
étape 2 : On reconnaît la formule du nombre dérivé de la fonction ln en 1.
La fonction ln a pour dérivée la fonction 1x qui prend donc la valeur 1 lorsque x=1.
Conclusion : limh→0ln(1+h)−ln1(1+h)−1=limh→0ln(1+h)h=1.
Propriétés algébriques
La fonction logarithme népérien
Définition
La fonction logarithme népérien est la fonction f définie et dérivable sur ]0;+∞[ tel que
f(1)=0 et f′(x)=1x
ln est la primitive de x↦1x sur ]0;+∞[ qui s’annule en 1.
Propriétés algébriques
Pour tous réels x>0 et y>0 :
ln(xy)=lnx+lny
ln(1x)=−lnx
ln(xy)=lnx−lny
ln(xn)=nlnx avec n ϵ Z
Exemple :
Réduire : A=ln8−3ln16 et B= 4ln9+5ln27ln3.
étape 1: On réécrit l’expression A pour faire apparaître ln2.
A=ln23−3ln24
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
ln(xn)=nlnx avec n∈Z.
A=3ln2−12ln2
A=−9ln2
étape 3: On réécrit l’expression B pour faire apparaître ln3.
B= 4ln32+5ln33ln3
étape 4 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
ln(xn)=nlnx avec n∈Z.
B= 8ln3+15ln3ln3
On factorise par ln3 pour finir le calcul.
B= 23ln3ln3
B= 23
Autre exemple :
Simplifier : C= ln(x+3)+ln2−2ln(x+1) en précisant l’intervalle d’étude.
étape 1 : On précise l’ensemble de définition de l’expression.
x doit vérifier x+3>0 et x+1>0, c’est-à-dire :
x>−3 et x>−1.
La condition finale est donc: x>−1.
étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :
- ln(xy)=lnx+lny,
- ln(xy)=lnx−lny
- ln(xn)=nlnx avec n∈Z
Ainsi,
C= ln(2x+6)−ln(x+1)2
C= ln2x+6(x+1)2
Équations, inéquations et logarithme népérien
Résolutions d’équations et inéquations avec la fonction ln
Liens avec la fonction exponentielle :
Pour tout réel x, ln(ex)=x.
Pour tout réel x>0, elnx=x.
Equations
Pour tous réels x>0 et y>0,
lnx=lny⟺x=y.
Pour tout réel x>0 et tout réel a,
lnx=a⟺x=ea.
Inéquations
Pour tous réels x>0 et y>0,
lnx<lny⟺x<y.
Pour tout réel x>0 et tout réel a,
lnx<a⟺x<ea.
Exemple
Résoudre 3ln(x+1)−3=0 en précisant l’ensemble d’étude.
étape 1 :
On n’oublie pas de préciser l’ensemble de définition sur lequel on travaille.
x doit vérifier : x+1>0 soit : x>−1.
On cherche donc des solutions sur ]−1;+∞[.
étape 2 :
On se ramène à une écriture du type : lnx=lny en utilisant lne=1.
3ln(x+1)=3
ln(x+1)=1
ln(x+1)=lne
étape 3 :
On sait que lnx=lny⟺x=y Ainsi :
x+1=e
x=e−1
étape 4 :
On conclut en donnant l’ensemble des solutions.
S={e−1}
Autre exemple
Résoudre sur ]−1;+∞[ :
ln(x+3)−2ln(x+1)⩽0
étape 1 :
On sait que lnx⩽lny⟺x⩽y donc on réécrit l’expression pour faire apparaître l’inéquation entre deux logarithmes.
ln(x+3)⩽2ln(x+1) soit
ln(x+3)⩽ln(x+1)2
étape 2 :
On applique les propriétés du logarithme sur les inéquations.
ln(x+3)⩽ln(x+1)2⟺(x+3)⩽(x+1)2
x+3⩽x2+2x+1
x2+x−2⩾0
étape 3 :
On remarque que 1 est une solution évidente du trinôme où on calcule son discriminant et on trouve que 1 et −2 sont les racines de x2+x−2.
étape 4 :
Pour déterminer le signe du trinôme, on utilise un tableau de signes uniquement sur l’ensemble de définition.
La racine x=−2 n’apparait donc pas :

étape 5 :
On fait attention à l’ensemble de définition de départ avant de conclure.
S=[1;+∞[
Fonctions composées - ln (u(x))
Fonctions composées ln(u(x))
Théorème
Soit la fonction f définie sur l’intervalle I par:
f(x)=ln(u(x)) où u est une fonction dérivable et strictement positive sur I,
alors f est dérivable sur I et f′(x)=u′(x)u(x).
Exemple
Déterminer l’ensemble de définition et la dérivée de la fonction f définie par :
f(x)=ln(x2+x+1)
Le discriminant Δ=1−4=−3 donc
x2+x+1>0.
La fonction est donc définie et dérivable sur R.
Pour tout x∈R, on a :
u(x)=x2+x+1 et u′(x)=2x+1.
Alors : f′(x)=2x+1x2+x+1.
Pour étudier les variations de cette fonction, on pourra juste étudier le signe de 2x+1