Formules des probabilités
Formules des probabilités
Définition
Soient $A$ et $B$ deux événements de $\Omega$, l’ensemble des issues d’une expérience aléatoire.
La probabilité d’un événement $P(A)$ se calcule grâce au quotient suivant :
$P(A) = \dfrac{\text{nombre d’éléments de } A}{\text{nombre d’issues de } \Omega}$.
En outre, une probabilité est toujours comprise entre 0 et 1 (le nombre d’issues de $A$ ne peut être négatif et il ne peut pas dépasser le nombre d’éléments de $\Omega$).
Propriétés
La probabilité de l’ensemble vide vaut 0 : $P(\varnothing) = 0$.
La probabilité de $\Omega$ vaut 1 : $P(\Omega) = 1$.
Par exemple, si on considère l’expérience du lancé de dé, l’univers $\Omega$ est l’ensemble des entiers compris entre 1 et 6, donc
$P(\Omega) = \dfrac{\text{nombre d’issues de } A}{\text{nombre d’issues de } \Omega} = \dfrac{6}{6} = 1$.
Événement contraire
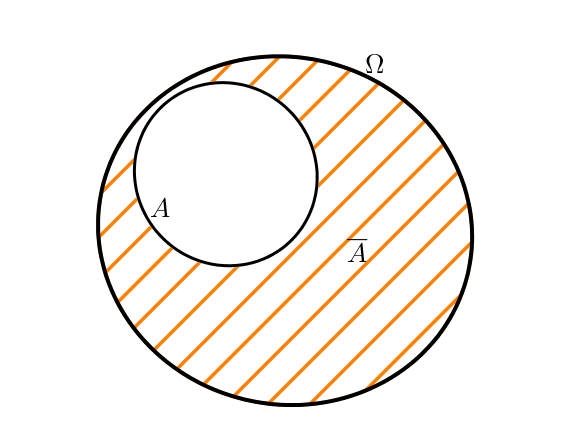
La probabilité de l’événement contraire à $A$, noté $\overline{A}$ et contenant toutes les issues n’appartenant pas à $A$, vaut
$P(\overline{A}) = 1 – P(A)$.
Probabilité de la réunion de deux événements
Pour calculer la probabilité de la réunion de deux événements, il est possible de compter le nombre d’issues appartenant à la réunion mais il existe aussi une formule :
$P(A \cup B) = P(A) + P(B) – P(A \cap B)$.
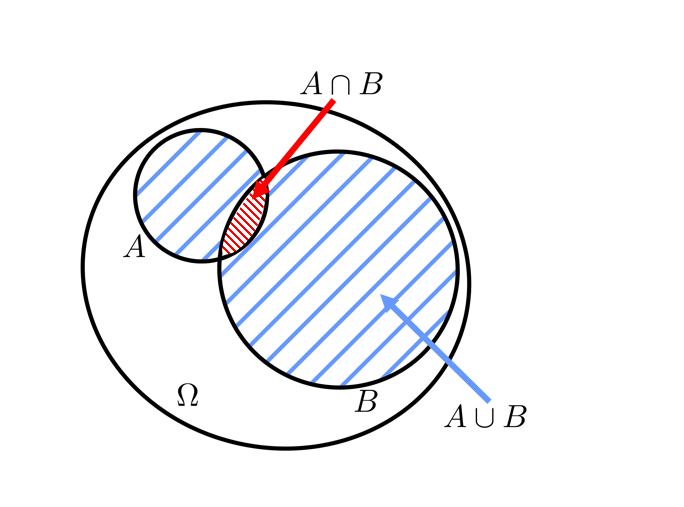
Cette formule dit que la probabilité de la réunion est égale à la somme des probabilités des deux événements à laquelle on soustrait la probabilité de l’intersection car on avait compté deux fois les issues appartenant à la fois à $A$ et à la fois à $B$ (on les avait ajoutées lors du calcul de $P(A)$ puis on les avait ajoutées à nouveau pour le calcul de $P(B)$).
Exemple :
On lance un dé à 6 faces.
On considère les événements
$A = “\text{obtenir un nombre pair}”$
$B = \text{“obtenir un nombre plus grand que 5”}$.
On cherche à calculer $P(A\cup B)$ :
$P(A\cup B) = P(A) + P(B) – P(A \cap B)$.
Or il y a trois nombres pairs possibles (2; 4; 6), donc $P(A) = \dfrac{3}{6} = \dfrac{1}{2}$.
Et il y a deux nombres plus grands que 5 ainsi $P(B) = \dfrac{2}{6} = \dfrac{1}{3}$.
Aussi, il existe un nombre pair et plus grand que 5 (c’est le nombre 6), donc $P(A \cap B) = \dfrac{1}{6}$.
Ainsi, $P(A\cup B) = \dfrac{1}{2} + \dfrac{1}{3} – \dfrac{1}{6} = \dfrac{2}{3}$.
Il était également possible de compter directement les issues appartenant à $A \cup B = \{2; 4; 5; 6\}$.
Ainsi, $P(A\cup B) = \dfrac{4}{6} = \dfrac{2}{3}$
Arbres et tableaux - Le rappel de cours
Probabilités : Arbres et tableaux
Dans une assemblée de 200 femmes, on remarque celles ayant un chapeau ou ayant les yeux bleus.
Il y a 90 femmes qui ont les yeux bleus dont 40 avec un chapeau et 120 femmes qui portent un chapeau.
Il est possible de représenter la situation décrite par l’énoncé sous la forme d’un arbre ou d’un tableau.
Il faut cependant d’abord analyser les données de l’énoncé.
L’univers de l’étude $\Omega$ est les 200 femmes.
On étudie deux événements :
$C = \text{“Avoir un chapeau”}$
$B = \text{“Avoir les yeux bleus”}$.
Généralement, on indique dans l’arbre des probabilités alors que dans le tableau on écrit des effectifs.
Arbre
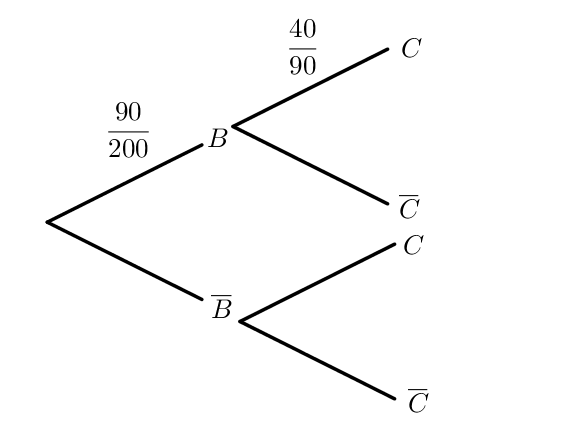
On indique sur les branches la probabilité de l’événement correspondant situé à l’extrémité droite de ces dernières.
Ici, de chaque noeud partent deux branches qui correspondent à l’événement et à son contraire.
Le texte donne la proportion de femmes avec des yeux bleus en premier.
On commence ainsi par calculer $p(B) = \dfrac{90}{200}$ que l’on indique sur la branche.
Or on sait que parmi ces 90 personnes, 40 portent un chapeau.
Ainsi, sur la branche $C$ partant de $B$, on doit indiquer la proportion de personne portant un chapeau et ayant les yeux bleus, c’est à dire $\dfrac{40}{90}$.
On remarquera donc que l’on n’a pas indiqué pas la probabilité de l’événement $C$ ici, car $C$ apparait deux fois : certaines femmes n’ont pas les yeux bleus mais portent un chapeau.
Tableau
On sait que le total de femmes ayant les yeux bleus est de 90.
On sait aussi qu’il y a 40 personne avec les yeux bleus et un chapeau, ainsi à l’intersection de la ligne $B$ et de la colonne $C$ on indique 40.
On sait aussi qu’il y a 120 femmes qui ont un chapeau. Ainsi, on indique un total de 120 dans la colonne de $C$
| $C$ | $\overline{C}$ | Total | |
| $B$ | 40 | 90 | |
| $\overline{B}$ | |||
| Total | 120 | 200 |
Dans les deux cas, le reste des informations se déduit en faisant des calculs.
Ainsi, on sait qu’il y a 90 femmes qui ont les yeux bleus et que parmi elles, 40 ont un chapeau : on en déduit que 50 femmes n’ont pas de chapeau dans cette catégorie.
En outre, on en conclut aussi qu’il y a 200 – 90 = 110 femmes qui n’ont pas les yeux bleus.
Donc $p(\overline{B}) = \dfrac{110}{200}$.
On sait aussi qu’il y a 120 personnes qui ont un chapeau et on cherche combien ont un chapeau mais pas les yeux bleus en sachant combien ont un chapeau et les yeux bleus (40) ainsi on trouve la donnée manquante par 120 – 40 = 80.
Enfin, on obtient le nombre de personnes n’ayant ni les yeux bleus ni un chapeau en effectuant le calcul suivant : 110 – 80 = 30 femmes.
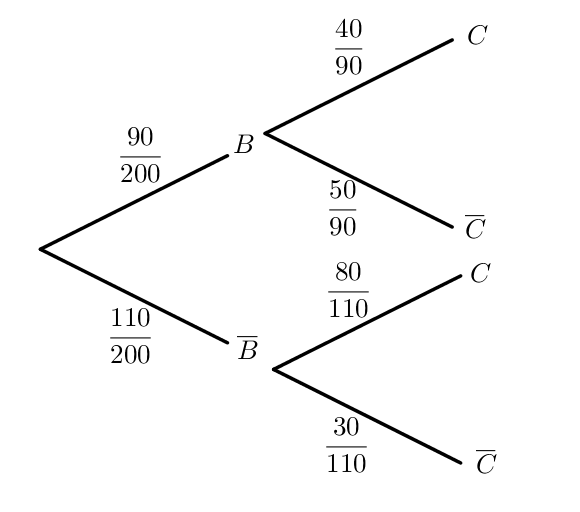
Après calculs, on obtient les arbre et tableau suivants :
| $C$ | $\overline{C}$ | Total | |
| $B$ | 40 | 50 | 90 |
| $\overline{B}$ | 80 | 30 | 110 |
| Total | 120 | 80 | 200 |
Loi de probabilité
Loi de probabilité
Considérons l’exemple suivant :
Une boite contient 10 billes : 4 rouges, 5 vertes et 1 jaune.
On s’intéresse à l’expérience aléatoire suivante : on tire une bille au hasard et on note sa couleur. A partir de cette expérience est défini l’univers, on peut soit obtenir une boule rouge, soit une boule verte soit une boule jaune ainsi
$\Omega = \{R; V; J \}$.
Définition
On cherche à déterminer les probabilités correspondantes à chaque issue de l’univers : c’est la loi de probabilité, que l’on présente sous forme de tableau.
Ainsi à chaque événement est associé un réel $p$ tel que $0 \leq p \leq 1$, c’est la probabilité de l’événement considéré.
De plus, la somme des toutes les probabilités est égale à 1.
On calcule donc séparément chacune des probabilités.
La probabilité d’obtenir une bille rouge correspond au rapport du nombre de billes rouges par le nombre total de billes, ainsi
$P(B) = \dfrac{4}{10} = \dfrac{2}{5}$.
De même, $P(V) = \dfrac{5}{10} = \dfrac{1}{2}$ et
$P(J) = \dfrac{1}{10}$.
La loi de probabilité est donc :
| Issue | $R$ | $V$ | $J$ |
| Probabilité | $\dfrac{2}{5}$ | $\dfrac{1}{2}$ | $\dfrac{1}{10}$ |
On peut alors vérifier que
$P(R) + P(V) + P(J) = \dfrac{2}{5} + \dfrac{1}{2} + \dfrac{1}{10} = \dfrac{10}{10} = 1$.
Intersection et réunion d'événements
Intersection et réunion d’événements
Pour introduire la notion d’intersection et de réunion, on considère un exemple.
On lance deux dés et on s’intéresse à la somme des points obtenus.
Les issues possibles, l’univers, sont $\Omega = \{2; 3; 4; 5; …; 12 \}$.
On définit l’événement $A$ qui est d’obtenir une somme paire :
$A = \{2; 4; 6; 8; 10; 12 \}$ et l’événement $B$ qui est d’obtenir une somme supérieure ou égale à 7 :
$B = \{7; 8; 9; 10; 11; 12 \}$.
L’intersection
L’intersection de deux droites est le point appartenant à la fois à la droite $(d_1)$ et à la droite $(d_2)$.
L’intersection de deux événements, notée $A \cap B$ ($A$ inter $B$), correspond donc à toutes les issues communes aux événements $A$ et $B$.
Ici, $A \cap B = \{8; 10; 12 \}$.
La réunion
La réunion de deux événements, notée $A \cup B$ ($A$ union $B$), correspond à toutes les issues appartenant à $A$ ou à $B$.
Il faudra cependant éviter d’écrire deux fois les issues appartenant aux deux événements.
Ici, $A \cup B = \{2; 4; 6; 7; 8; 9; 10; 11; 12 \}$.
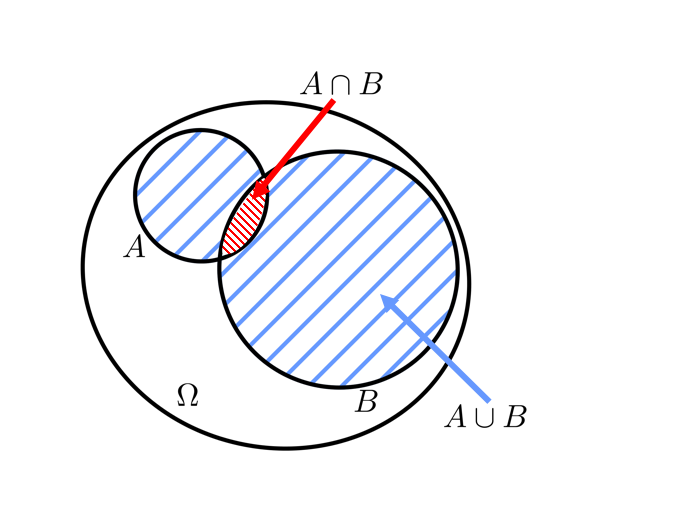
Vocabulaire des probabilités
Vocabulaire des probabilités
Afin d’introduire le vocabulaire lié aux probabilités, on considère l’exemple suivant :
On lance deux dés non truqués et on s’intéresse à la somme des points obtenus : il s’agit donc d’une expérience aléatoire dont on connait les résultats mais dont on ignore lequel se réalise.
L’ensemble des résultats possibles, c’est à dire toutes les issues possibles, s’appelle l’univers et est noté $\Omega$.
Ici, $\Omega = \{2; 3; 4; 5; …; 12\}$, c’est à dire tous les entiers compris entre 2 et 12.
Il est possible de définir un sous-ensemble de $\Omega$, appelé événement, comme par exemple l’événement $A$ qui est d’obtenir une somme paire :
$A = \{2; 4; 6; 8; 10; 12 \}$ ou encore l’événement $B$ qui est d’obtenir une somme égale à 10 :
$B = \{10 \}$.
$B$ est un événement élémentaire, c’est à dire qui ne contient qu’un seul résultat.
Un événement certain est un événement qui se réalise forcément : par exemple l’événement $\Omega$ est un événement certain : la somme est forcément comprise entre 2 et 12 quelque soit le résultat du lancé.
Un événement impossible est un événement qui ne peut pas se réaliser,
l’événement $C = \{13 \}$ est un événement impossible par exemple.
L’événement contraire à un événement $D$ est l’ensemble des issues appartenant à $\Omega$ mais qui n’appartiennent pas à $D$.
On note cet événement $\overline{D}$, qu’on lit “$D$ barre”.
Par exemple $\overline{A} = \text{“obtenir une somme impaire”} = \{3; 5; 7; 9; 11 \}$.
