Fonction racine carrée
Fonction racine carrée
Définition
La fonction racine carrée est une fonction définie sur R+ à valeurs dans R+ et on la note {f:R+→R+x↦√x
La racine carrée d’un nombre négatif n’existe donc pas et le résultat est obligatoirement positif ou nul.
Variations
La fonction est strictement croissante et son tableau de variations est le suivant :

La démonstration de la croissance de la fonction racine carrée est exigible.
Soient a et b deux réels positifs tel que a<b,
On souhaite montrer que √a<√b.
Pour cela, on étudie le signe de la différence √b–√a.
On utilise donc l’expression conjuguée :
√b–√a=(√b–√a)(√b+√a)√a+√b=b–a√a+√b
Or b>a donc b–a>0. De plus, √a+√b est toujours positif.
Ainsi, b–a√a+√b>0 ce qui revient à dire que √b–√a>0 ou encore √b>√a.
Représentation graphique
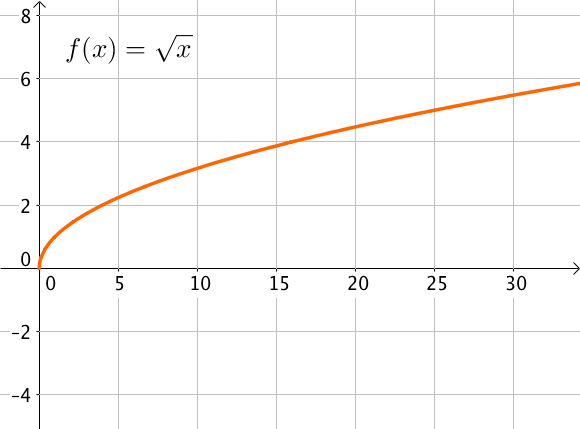
La position de la courbe représentation de la fonction racine carrée par rapport aux fonctions y=x et y=x2 est aussi à connaitre.
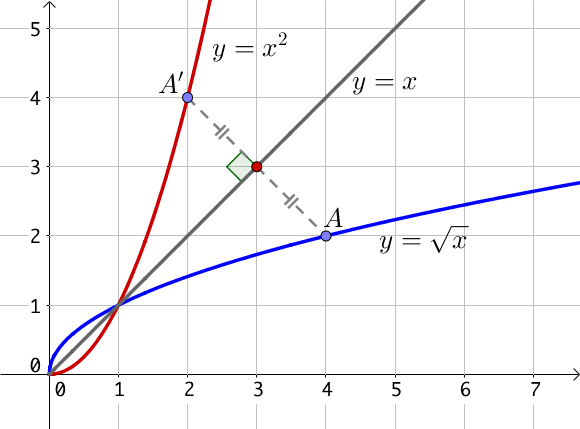
On remarque dans un premier temps que les fonctions y=x2 et y=√x sont symétriques par rapport à la droite d’équation y=x.
Pour 0≤x≤1, la fonction y=√x est au dessus de la fonction y=x elle même au dessus de la fonction y=x2.
Pour x≥1, l’ordre est inversé.
Les démonstrations de ces positions sont exigibles.
Pour étudier la position, on étudie le signe de f(x)–g(x) où f et g sont deux fonctions parmi les trois en utilisant la quantité conjuguée lorsque l’une des fonctions sera la fonction racine carrée.
Etudions par exemple la position relative de y=x par rapport à y=√x. On étudie alors le signe de x–√x:
Soit x∈R+, x–√x≥0⟺x2–xx+√x⟺x2–x≥0⟺x(x–1)≥0⟺x–1≥0 (car x est toujours positif).
Ainsi, pour x≥1, la fonction y=x est au dessus de la fonction racine carrée.
Pour x≤1, la fonction racine carrée est au dessus de la fonction y=x.
Fonction cube
Fonction cube
Définition
La fonction cube est une fonction définie sur R à valeurs dans R et se note {f:R→Rx↦x3.
Variations
Cette fonction est strictement croissante pour tout réel x.

La représentation graphique de la fonction cube est la suivante :
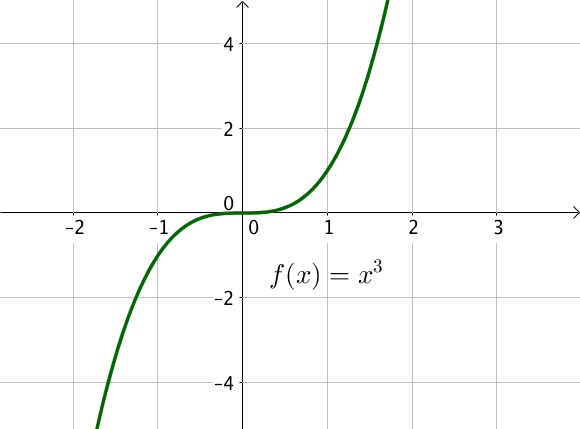
A retenir :
Pour tout x≥0, x3≥0
Pour tout x≤0, x3≤0.
Les fonctions u et u3 ont les mêmes variations.
Par exemple, pour étudier les variations de (x+3)3, on peut étudier les variations de x+3 puis en déduire celle de (x+3)3.
Or on sait que x+3 est une fonction croissante sur R, ainsi, (x+3)3 est aussi une fonction croissante.
Pour tous réels a et b,
a3–b3=(a–b)(a2+ab+b2).
Fonction valeur absolue
Fonction Valeur absolue
Définition
La fonction valeur absolue est une fonction définie sur R à valeur dans R+ et on la note {f:R→R+x↦|x|.
La valeur absolue d’un nombre positif est le nombre lui-même.
La valeur absolue d’un nombre négatif est son opposé.
En d’autres termes,
Si x≥0, |x|=x
Si x≤0, |x|=−x
La fonction est strictement décroissante pour x négatif et strictement croissante pour x positif.

Sa représentation graphique est la suivante :
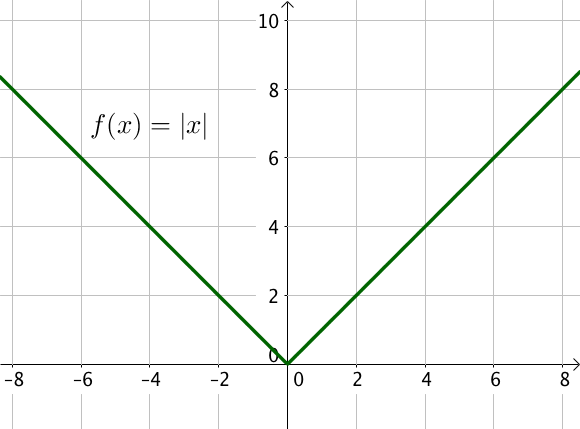
Propriétés
Pour tout x∈R,√x2=|x|.
Par exemple, √(−4)2=4=|−4|.
Exemples :
|−5|=5
|7|=7
|√2–5|=–√2+5
|π+2|=π+2
|π–4|=4–π
Pour étudier la fonction f(x)=|x+3|, on étudie le signe de x+3 en s’aidant d’un tableau de signe.
Si x+3≥0 alors f(x)=x+3. Si x+3≤0 alors f(x)=−(x+3).


