Quatrième proportionnelle
Quatrième proportionnelle
Définition
Soient A et B deux grandeurs proportionnelles.
On dispose du tableau de proportionnalité suivant :
| A | 5 | 3 |
| B | 7 | x |
On cherche la valeur de x, en connaissant trois valeurs : c’est la quatrième proportionnelle.
Méthodes
La première méthode consiste à trouver le coefficient de proportionnalité qui permet de passer de la première ligne à la seconde et qui vaut 75.
Ainsi, x=3×75
x=215=4,2
La seconde méthode consiste à trouver le coefficient qui permet de passer de la première colonne à la deuxième : ce dernier vaut 35.
Ainsi,
x=7×35
x=215=4,2
Dans tous les cas, x=3×75.
On représente généralement ce calcul par la flèche suivante :
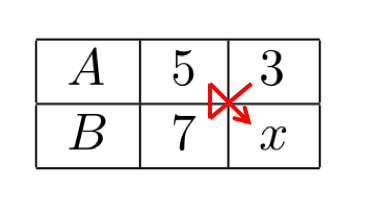
Cela signifie que l’on part de 3 puis que l’on multiplie par 7 et enfin que l’on divise par 5 pour trouver x.
On retiendra que :
x=3×75
Exemples
1) On achète 2,3 kg de pommes à 1,90 € le kg.
On sait que le prix est proportionnelle à la masse de pommes achetées, on utilise donc un tableau de proportionnalité.
| Prix (en €) | 1,9 | x? |
| Masse (en kg) | 1 | 2,3 |
Pour trouver x, on peut calculer le coefficient de proportionnalité.
On utilise ici la méthode présentée précédemment.
On trouve alors :
x=1,9×2,31=4,37
On paie donc 4,37 €.
2) On achète 7 cahiers identiques pour 20,65€. Combien doit-on payer si on achète seulement 3 cahiers ?
Comme les cahiers sont identiques, il y a proportionnalité entre le prix et le nombre de cahiers achetés. On utilise donc un tableau de proportionnalité.
| Prix (en €) | 20,65 | x |
| Nombre de cahiers | 7 | 3 |
En appliquant la méthode, on trouve :
x=20,65×37=8,85
Si on achète 3 cahiers, on paie 8,85 €.
