Forme canonique

Forme canonique

Forme canonique

Une fonction polynomiale de degré 2 définie sur $\mathbb{R}$ s’écrit sous la forme $f(x) = ax^2 + bx + c$, avec $a \neq 0$.

Sa représentation graphique est une parabole tournée vers le haut ou le bas selon le signe de $a$.

Cette fonction admet une autre écriture de la forme $f(x) = a(x -\alpha)^2 + \beta$ avec $\alpha, \beta \in \mathbb{R}$ : c’est la forme canonique.

Considérons l’exemple suivant : $f(x) = 2x^2 – 4x + 5$ pour $x \in \mathbb{R}$.

La première étape afin de parvenir à la forme canonique de $f$ consiste à factoriser les termes en $x$ et $x^2$ par $a$.

Ainsi, $f(x) = 2(x^2 – 2x) + 5$. Il faudra prêter une attention particulière au signe de $a$.

Il s’agit maintenant de se remémorer les identités remarquables :
$(a + b)^2 = a^2 + 2ab + b^2$ que l’on réécrit sous la forme $(a + b)^2 – b^2 = a^2 + 2ab$.

Ainsi, $x^2 – 2x$ correspond au début de l’identité remarquable ($a^2 + 2ab$) que l’on réécrit sous la forme $x^2 – 2 \times 1 \times x$.

Ainsi, $a = x$ et $b = -1$ et on trouve alors $f(x) = 2 \left[(x – 1)^2 – 1\right] + 5$.

Enfin, on réécrit $f$ sous la forme $f(x) = 2(x – 1)^2 – 2 + 5 = 2(x – 1)^2 + 3$. C’est donc la forme canonique, avec $\alpha = 1$ et $\beta = 3$.

Graphiquement, on obtient :

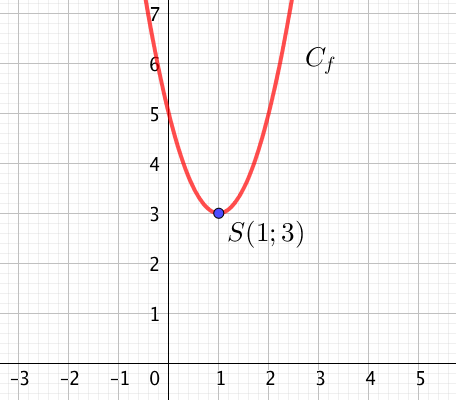
Afin de s’assurer que la forme canonique est correcte, on peut développer à nouveau l’identité remarquable pour retrouver la forme initiale de $f$.