Fonctions convexes, concaves

Fonctions convexes et concaves

Fonctions convexes et concaves

Définition

Soit $f$ une fonction dérivable sur un intervalle $I$,

$f$ est convexe sur $I$ lorsque sa courbe est entièrement située au dessus de chacune de ses tangentes.

Il s’agit donc d’une notion locale, définie sur un intervalle.

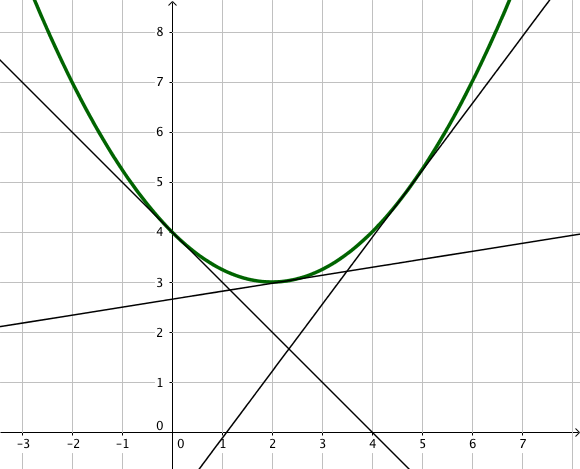
Par exemple, la fonction $y = x^2$ est convexe sur $\mathbb{R}$.

Pour démonter la convexité d’une fonction, on utilisera d’autres propriétés plus efficaces que cette notion graphique. 

$f$ est concave sur $I$ lorsque sa courbe est entièrement située en dessous de chacune de ses tangentes.

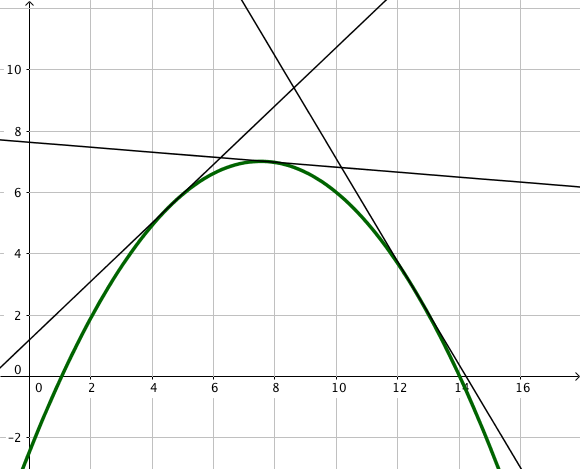
Par exemple, la fonction $y= \sqrt{x}$ est concave sur $\mathbb{R}^+_*$