Fonction valeur absolue
Fonction Valeur absolue
Définition
La fonction valeur absolue est une fonction définie sur R à valeur dans R+ et on la note {f:R→R+x↦|x|.
La valeur absolue d’un nombre positif est le nombre lui-même.
La valeur absolue d’un nombre négatif est son opposé.
En d’autres termes,
Si x≥0, |x|=x
Si x≤0, |x|=−x
La fonction est strictement décroissante pour x négatif et strictement croissante pour x positif.

Sa représentation graphique est la suivante :
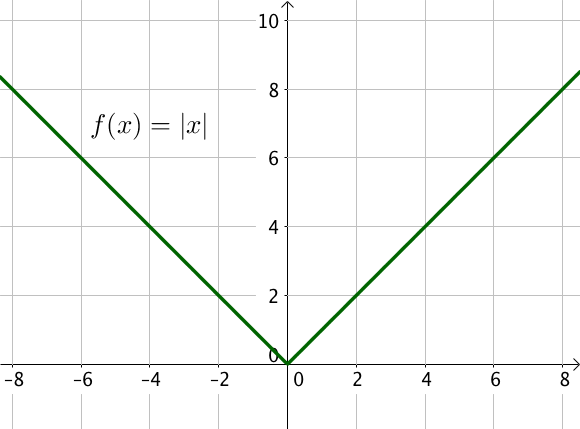
Propriétés
Pour tout x∈R,√x2=|x|.
Par exemple, √(−4)2=4=|−4|.
Exemples :
|−5|=5
|7|=7
|√2–5|=–√2+5
|π+2|=π+2
|π–4|=4–π
Pour étudier la fonction f(x)=|x+3|, on étudie le signe de x+3 en s’aidant d’un tableau de signe.
Si x+3≥0 alors f(x)=x+3. Si x+3≤0 alors f(x)=−(x+3).
