Développer et factoriser

Développer et factoriser k(a+b)

Développer et factoriser $k(a + b)$.

Définitions

$k(a +b)$ se lit $k$ facteur de $(a + b)$ où $a$, $b$ et $k$ sont trois nombres.

• Développer

Cela revient à distribuer $k$ à chacun des termes présents entre parenthèse. 

Ainsi,

$k(a + b) = k\times a + k\times b$. 

Développer permet donc de transformer un produit en une somme. 

• Factoriser

A l’inverse, si on utilise l’égalité dans le sens suivant :

$k\times a + k\times b = k(a + b)$

On passe d’une somme à un produit : c’est la factorisation. 

Pour factoriser une expression, il faut faire apparaitre le facteur commun aux deux termes de la somme.

Exemples :

• a) Développer $5(x  + 2)$.

On distribue donc $5$ à $x$ puis à $2$. Ainsi,

$5(x  + 2) = 5\times x + 5\times 2$

$5(x  + 2)= 5x + 10$.

• b) Développer $7(8  – x)$

On distribue donc $7$ à $8$ puis à $x$. Ainsi,

$7(8  – x) = 7\times 8 – 7\times x$

$7(8  – x) = 56 – 7x$

• c) Factoriser $6x + 12$

On remarque que $12 = 6 \times 2$, $6$ est donc le facteur commun. Ainsi,

$6x + 12 = 6\times x + 6 \times 2$

$6x + 12 = 6(x + 2)$.

En développant cette expression, on retrouve l’expression initiale.

• d) Factoriser $21 – 7x$.

On remarque que $21$ est un multiple de $7$, donc $7$ est le facteur commun.

$21 – 7x = 7 \times 3 – 7 \times x$

$21 – 7x = 7 ( 3 -x )$. 

• e) Factoriser $3 + 3x$.

Le facteur commun est $3$. Il faut cependant faire apparaitre dans chacun des termes un produit faisant intervenir $3$.

On se rappelle alors que $3 = 3 \times 1$.  Ainsi,

$3 + 3x = 3\times 1 + 3 \times x

$3 + 3x= 3 (1 + x)$

Remarques :

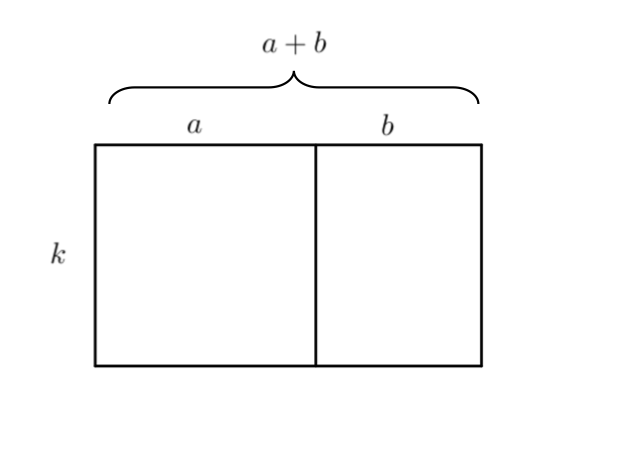
On peut retrouver ce résultat à l’aide d’un rectangle de longueur $a + b$ et de largeur $k$.

Pour calculer l’aire de ce rectangle, on effectue le produit de la longueur par la largeur, c’est à dire $k(a + b)$.

Ou bien, on peut diviser le rectangle en deux rectangle de longueur $a$ et $b$, et l’aire vaut alors $ka + kb$, c’est à dire la somme des aires des deux rectangles. 

Mais comme il s’agit du même rectangle, on a bien

$k(a + b) = ka + kb$. 

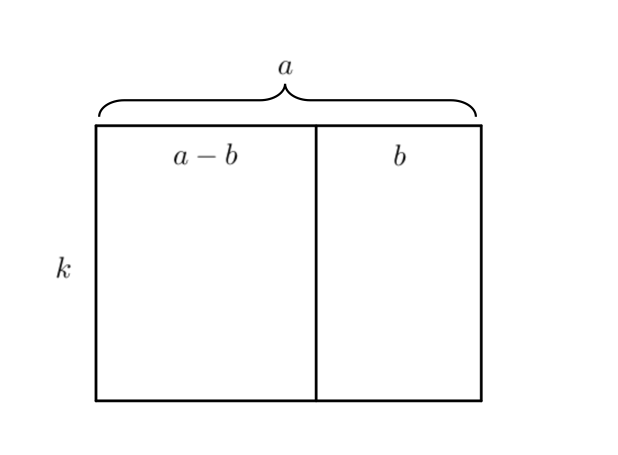
Si l’addition se transforme en soustraction, on a alors la formule suivante : 

$k(a – b) = k\times a – k\times b$

Pour comprendre cette égalité, on peut aussi se référer à une situation géométrique. 

On cherche ici à calculer l’aire du rectangle de longueur $a – b$ qui vaut $k(a -b)$.

Mais ce même calcul peut se faire en calculant l’aire du grand rectangle de longueur $a$ qui vaut $ka$ et en lui soustrayant l’aire du rectangle de côté $b$ valant $kb$, c’est à dire $ka – kb$.