Dérivée seconde et position d'une courbe par rapport à ses tangentes
Dérivée seconde et position d’une courbe par rapport à ses tangentes
Soit f une fonction deux fois dérivable sur un intervalle I et x0∈I.
Soit Γf la courbe représentative de la fonction f dans le repère (O;→i;→j) et MO(x0,f(x0)).
On note Δ la tangente à ΓF en M0 (cette tangente existe car f est dérivable en x0).
Soit x∈I et M(x,f(x)),
Soit T le point de Δ tel que T(x,yT),
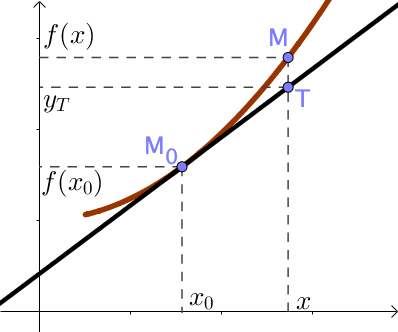
On étudie ici la position de la courbe par rapport à sa tangente en un point d’abscisse x0 quelconque. Pour cela, on étudie l’ordonnée du vecteur →TM (l’abscisse du vecteur étant nulle) à partir d’un point M quelconque :
y→TM=yM–yT=f(x)–yT.
Or T est un point de la tangente Δ dont on connait l’équation :
y=f(x0)+(x–x0)f′(x0).
Ainsi, yT=f(x0)+(x–x0)f′(x0).
Finalement, y→TM=f(x)–f(x0)–(x–x0)f′(x0).
On note alors δ(x)=f(x)–f(x0)–(x–x0)f′(x0) et on étudie le signe de cette fonction. Pour cela, on étudie ses variations. La fonction δ est dérivable sur I en tant que somme de fonctions dérivables sur I :
δ′(x)=f′(x)–f′(x0).
Pour étudier le signe de δ′(x), on fait tout d’abord l’hypothèse que f”≥0 sur I, c’est à dire que f′ est croissante sur I.
Ainsi, pour x≥x0,f′(x)≥f′(x0) c’est à dire δ′(x)≥0.
De même, pour x≤x0,f′(x)≤f′(x0) c’est à dire δ′(x)≤0.
On en déduit alors le sens de variation de la fonction δ.
δ est décroissante pour x≤x0 et croissante pour x≥x0.
En outre, δ(x0)=f(x0)–f(x0)–(x0–x0)f′(x0)=0.
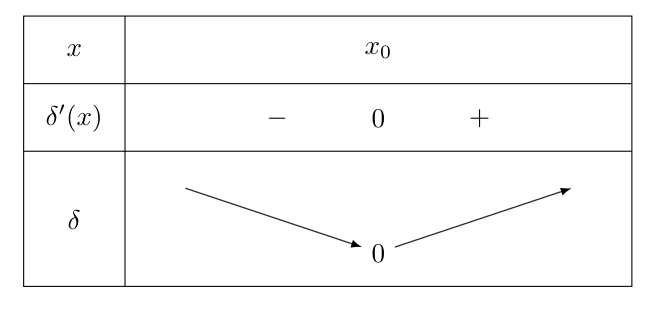
Finalement, δ≥0 ce qui signifie que l’ordonnée de →TM est positive et donc que M est au dessus de T.
Puisque ce raisonnement peut être fait pour tout x0∈I, on en déduit que lorsque f”≥0, la courbe est toute entière située au dessus de toutes ses tangentes. On dit que f est convexe.
De même, on peut s’intéresser à l’hypothèse de f”≤0 sur I, c’est à dire que f′ est décroissante sur I.
Ainsi, pour x≥x0,f′(x)≤f′(x0) c’est à dire δ′(x)≤0.
De même, pour x≤x0,f′(x)≥f′(x0) c’est à dire δ′(x)≥0.
On en déduit alors le sens de variation de la fonction δ.
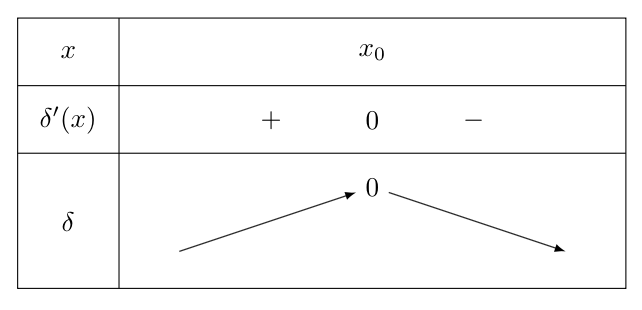
Ainsi, δ≤0 et M est sous T.
Puisque ce raisonnement peut être fait pour tout x0∈I, on en déduit que lorsque f”≤0, la courbe est toute entière située en dessous de toutes ses tangentes. On dit que f est concave.
Le dernier cas que l’on peut traiter correspond au cas où f” n’est pas de signe constant sur I et s’annule en x0 en changeant de signe. On se propose ici de traiter le cas où f” est d’abord négative puis positive.
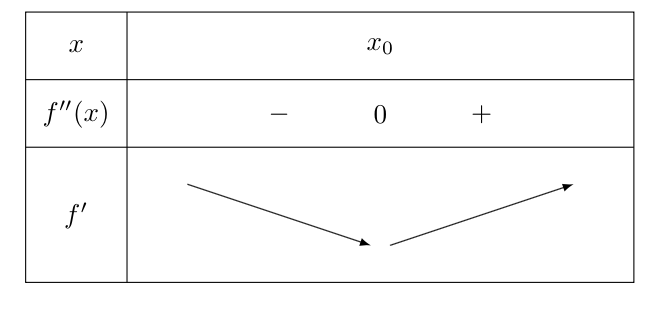
Ainsi, f′(x)≥f′(x0) pour tout x∈I. Donc δ′≥0. Ainsi δ est croissante sur I.
Or δ s’annule en x0. Donc pour x≤x0, δ est négative. Et pour x≥x0, δ est positive.
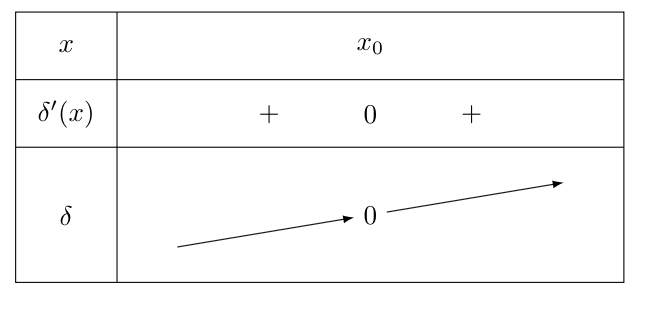
Graphiquement, pour x≤x0 la courbe de f est en dessous de ses tangentes.
Pour x≥x0, la courbe de f est au-dessus de ses tangentes.
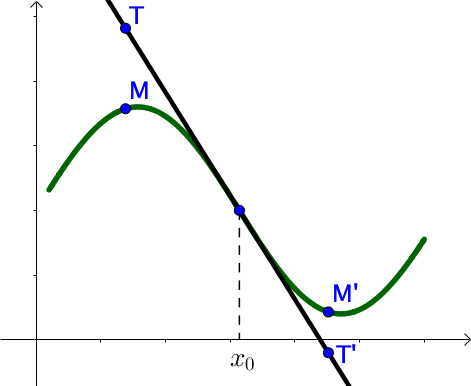
Ainsi, si f” s’annule en changeant de signe en x0, Γf traverse sa tangente en M0.
On dit que x0 est un point d’inflexion de f.
Dérivée seconde d'une fonction
Dérivée seconde d’une fonction
Définition
Soit f une fonction dérivable sur un intervalle I de R.
Si f′ est dérivable sur I, on note (f′)′=f” sa dérivée que l’on appelle dérivée seconde de f sur I.
Exemples :
- Soit f:x↦3x2+5x+7 une fonction polynomiale, définie et dérivable sur R.
Soit x∈R, f′(x)=6x+5
f′ est aussi une fonction polynomiale, elle est donc dérivable sur R.
Soit x∈R, f”(x)=6
- Soit g:x↦cos(5x+3) une fonction définie sur R et dérivable sur R en tant que composée de deux fonctions dérivables sur cet intervalle.
Soit x∈R, g′(x)=−5sin(5x+3).
g′ est aussi dérivable en tant que composée de deux fonctions dérivables sur R.
Ainsi, soit x∈R, g”(x)=−25cos(5x+3).
Propriétés
Soit λ∈R,
Si u et v sont dérivables deux fois sur I,
Alors (λu+v) et (uv) sont deux fois dérivables sur I.
Les formules de la dérivée seconde du produit et de la somme ne sont pas à connaitre.
