Définition, propriétés

1
Définition du logarithme népérien
2
Propriétés analytiques
3
Propriétés algébriques

Définition du logarithme népérien

Définition

La fonction logarithme népérien est l’unique fonction $f$ , définie et dérivable sur $]0; +\infty[$ qui vérifie $\begin{array}{l} f(1) = 0 \\ f'(x) = \dfrac{1}{x} \end{array}$

On remarquera ici que l’on définit la fonction $f$ à partir de sa dérivée.

En outre, on peut noter que l’on ne connaissait jusqu’à présent pas de fonction dont la dérivée valait $\dfrac{1}{x}$ .

En supposant que le cours portant sur les intégrales a déjà été étudié, on peut alors définir la fonction logarithme népérien, que l’on note $\ln$ comme étant la primitive de $x \mapsto \dfrac{1}{x}$ sur $]0; +\infty[$ et qui s’annule en $1$ .

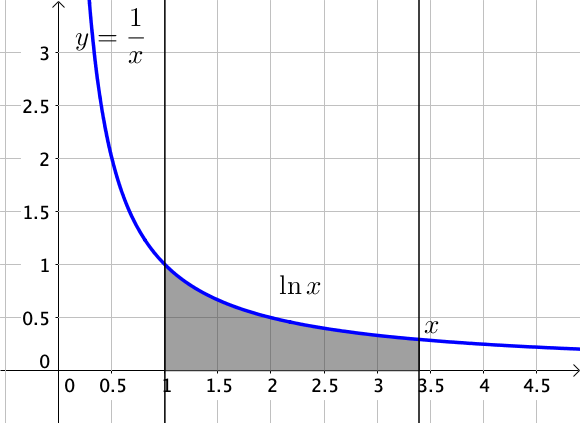
Ainsi, pour tout réel $x > 0$ ,
$\ln x = \displaystyle \int_1^x \dfrac{1}{t} dt$

On notera que lorsque $x = 1$ , $\ln 1 = \displaystyle \int_1^1 \dfrac{1}{t} dt = 0$ .

Graphiquement, la fonction $\ln x$ correspond à l’aire sous la courbe de la fonction inverse, comprise entre les droites verticales d’abscisse $1$ et $x$ .

Propriétés analytiques

La fonction $\ln$ est définie et dérivable sur $]0;+\infty[$ .

Pour tout réel $\displaystyle x>0, (\ln x)’= \dfrac{1}{x}$ .

La fonction $\ln$ est continue et strictement croissante sur $]0;+\infty[$ .

D’autre part,

$\ln (1)=0$

$\ln (e)=1$

$\displaystyle\lim\limits_{x \rightarrow +\infty} \ln x= +\infty$

$\displaystyle \lim_{\substack{x \to 0\\ x > 0}} \ln x=-\infty$

Variations et représentation graphique

Propriétés algébriques

La fonction logarithme népérien

Définition

La fonction logarithme népérien est la fonction $f$ définie et dérivable sur $]0;+\infty[$ tel que

$f(1)=0$ et $f'(x)=\dfrac{1}{x}$

$\ln$ est la primitive de $x\mapsto\dfrac{1}{x}$ sur $]0;+\infty[$ qui s’annule en 1.

Propriétés algébriques

Pour tous réels $x>0$ et $y>0$ :

$\ln (xy)= \ln x+\ln y$

$\displaystyle \ln ( \displaystyle\frac{1}{x}) = -\ln x$

$\displaystyle \ln ( \displaystyle\frac{x}{y}) = \ln x-\ln y$

$\displaystyle \ln ( x^n) = n \ln x$ avec n $\epsilon$ $\mathbb{Z}$

Exemple :

Réduire : $A=\ln8-3\ln16$ et $B$ = $\displaystyle \frac{4\ln9+5\ln27}{\ln3}$ .

étape 1: On réécrit l’expression $A$ pour faire apparaître $\ln 2$ .

$A=\ln 2^3-3\ln 2^4$

étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :

$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$ .

$A=3\ln 2-12\ln 2$

$A=-9\ln 2$

étape 3: On réécrit l’expression $B$ pour faire apparaître $\ln 3$ .

$B$ = $\displaystyle \frac{4\ln 3^2+5\ln 3^3}{\ln 3}$

étape 4 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :

$\displaystyle \ln (x^n)=n\ln x$ avec $\displaystyle n \in \mathbb{Z}$ .

$B$ = $\displaystyle \frac{8\ln 3+15\ln 3}{\ln 3}$

On factorise par $\ln 3$ pour finir le calcul.

$B$ = $\displaystyle \frac{23\ln 3}{\ln 3}$

$B$ = 23

Autre exemple :

Simplifier : $C$ = $\displaystyle \ln (x+3)+\ln 2-2\ln (x+1)$ en précisant l’intervalle d’étude.

étape 1 : On précise l’ensemble de définition de l’expression.

$x$ doit vérifier $x+3>0$ et $x+1>0$ , c’est-à-dire :

$x>-3$ et $x>-1$ .

La condition finale est donc: $x>-1$ .

étape 2 : On utilise les propriétés algébriques du logarithme népérien pour simplifier l’expression :

$\ln (xy)=\ln x+\ln y$ ,
$\ln (\displaystyle\frac{x}{y})=\ln x-\ln y$
$\ln (x^n)=n\ln x$ avec $n \in \mathbb{Z}$

Ainsi,

$C$ = $\displaystyle \ln (2x+6)-\ln (x+1)^2$

$C$ = $\displaystyle \ln {\frac{2x+6}{(x+1)^2}}$