Annale – Scratch, fonctions

Antécédent d'un nombre par une fonction

Antécédent d’un nombre par une fonction

Définition

Soit $f$ une fonction et deux réels $a$ et $b$ vérifiant $f(a)=b$

On dit que $b$ est l’image de $a$ par $f$. (c’est une valeur unique)

On dit que $a$ est un antécédent par $f$ de $b$. (il peut y en avoir plusieurs)

Exemples

Cherchons le ou les antécédents, s’ils existent de $14$

Cela revient à chercher l’heure à laquelle la température était de 14°C.

Pour ce faire, on se place sur l’axe des ordonnées (l’axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d’intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.

Ici, il y a deux points d’intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h.  

Il se peut que dans certains cas il n’y ait aucune solution. 

Mathématiquement, le fait qu’il ait fait 14°C à 12h et 18h se traduit par :

Les antécédents de 14 par la fonction $f$ sont 12 et 18.

Ou encore :  les solutions de l’équation $f(t) = 14$ sont $S = \{12; 18\}$.

Considérons l’équation $f(t) = 10$ : on cherche donc les antécédents de 10 par $f$.

Les solutions sont donc $S = \{0; 6; 24\}$. 

Considérons l’équation $f(t) = 16$ : on cherche donc les antécédents de 16 par $f$.

La température de 16°C n’étant jamais atteinte, cette équation n’admet pas de solution : 

$S = \varnothing$.

Agrandissement - Réduction

Agrandissement – Réduction

Propriétés

Lorsque l’on réalise un agrandissement ou une réduction d’une figure ou d’un solide, toutes les longueurs sont multipliées par un coefficient multiplicateur $k$.

Les aires sont multipliées par $k^2$ et les volumes sont multipliés par $k^3$. 

Lorsqu’il s’agit d’un agrandissement, le coefficient $k$ est supérieur strictement à 1.

Lorsqu’il s’agit d’une réduction, le coefficient $k$ est inférieur strictement à 1 et positif.

1)

Par exemple, le cube a été agrandit d’un coefficient égal à 3. Ses surfaces ont donc été multipliées par 9.

Le cube ainsi agrandi est donc 27 fois plus volumineux que le cube initial. 

2)

Le rayon de la boule a été réduit de moitié. Le coefficient multiplicateur est donc égal à 0,5 : le diamètre est deux fois plus petit.

La surface de la sphère est donc multipliée par $(0,5)^2=0,25$

Le volume de la boule est multiplié par $(0,5)^3=0,125$.  

Fonction linéaire, fonction affine

Fonction linéaire, fonction affine

Fonctions linéaires 

Une fonction linéaire est un procédé qui à un nombre $x$ associe un nombre $f(x)$ de la forme $f(x) = ax$ où $a$, le coefficient directeur, est un nombre donné et on la note $x  \xrightarrow{f} f(x) = ax$.

Une fonction linéaire aura pour représentation graphique une droite passant toujours par l’origine du repère, c’est à dire le point de coordonnées $(0; 0)$.

Selon la valeur de $a$, l’inclinaison de la droite sera différente : plus $a$ est grand (et positif), plus la droite monte, plus $a$ est petit et positif, moins la droite monte. Si $a$ est négatif, la droite descend.  

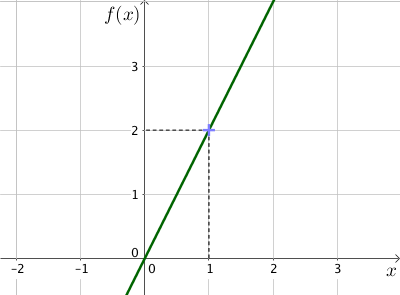
Sur le graphique, la fonction $f$ associe au nombre 1 le nombre 2.

Ainsi $f(1) = 2$.

Or la forme générale de $f$ est $f(x) = a \times x$ donc $f(1) = a \times 1 = a$ et $f(1) = 2$ donc $a = 2$.

Ainsi ce graphique est le représentation graphique de la fonction $f(x) = 2x$. 

Fonctions affines 

Une fonction affine est de la forme $x  \xrightarrow{f} f(x) = ax + b$ où $a$, le coefficient directeur, et $b$, l’ordonnée à l’origine, sont des nombres donnés.

$b$ s’appelle l‘ordonnée à l’origine car la représentation graphique des fonction affines est une droite qui coupe l’axe des ordonnées au point $b$.

La valeur de $a$ donne l’inclinaison de la droite. Plus $a$ est grand et positif, plus la droite monte; plus $a$ est petit, plus la droite descend. 

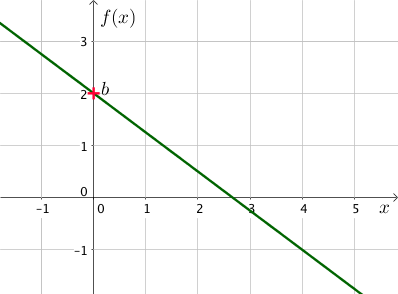
Enfin, les fonctions linéaires sont un cas particulier des fonctions affines, avec $b = 0$.

Déplacements

Boucles