Annale – Pythagore, Thalès, trigonométrie, transformations du plan
Théorème de Thalès
Théorème de Thalès
Il existe deux situations où l’on peut appliquer le théorème de Thalès qui sont représentées par le schémas ci-dessous.
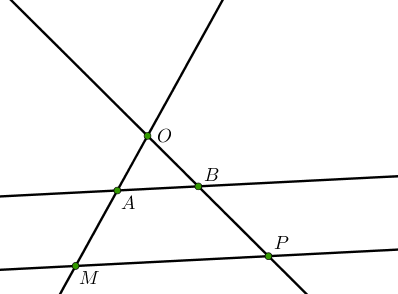
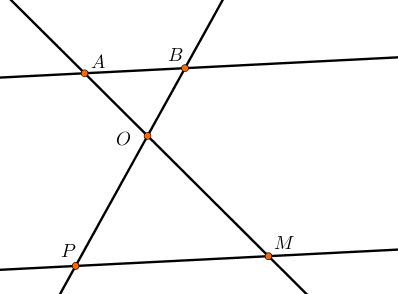
Deux droites doivent donc être sécantes et sont coupées par deux droites parallèles.
Théorème
Si O,A,M alignés
O,B,P alignés
(AB) // (MP)
Alors OAOM=OBOP=ABMP.
Le point O est appelé le point charnière.
Ce théorème permet d’obtenir des quotients de longueurs, permettant ainsi de trouver des d’autres longueurs.
Exemple :
Les points R,S,U sont alignés ainsi que les points T,R,V.
Les droites (ST) et (VU) sont parallèles. Donnons une valeur approchée de RV à 10−2.
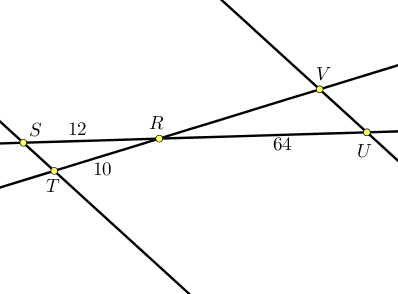
D’après le théorème de Thalès, RURS=RVRT=VUST.
6412=RV10
12×RV=10×64
RV=64012≈53,33
NB : à la toute fin de la vidéo, il y a une erreur de calcul, 640/12=53,3 et non 48 🙂 !!
Trigonométrie
Trigonométrie
La trigonométrie permet de mettre en relation des longueurs et des angles dans un triangle rectangle.
Vocabulaire
L’hypoténuse correspond au plus grand côté, en face de l’angle droit.
Le côté touchant l’angle ˆB autre que l’hypoténuse est appelé le côté adjacent.
Le côté en face de l’angle ˆB est appelé le côté opposé.
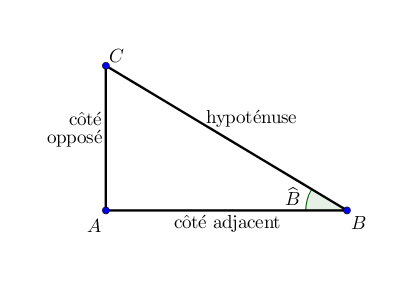
On définit ainsi le cosinus, le sinus et la tangente de l’angle ˆB par :
cosˆB=côté adjacenthypoténuse
sinˆB=côté opposéhypoténuse
tanˆB=côté opposécôté adjacent
Un moyen mnémotechnique pour se souvenir de ses définitions est :
CAH-SOH-TOA :
Cosinus = Adjacent divisé par l’Hypoténuse,
Sinus = Opposé divisé par l’Hypoténuse,
Tangente = Opposé divisé par Adjacent
Propriétés
Le cosinus et le sinus d’un angle sont reliés par la relation suivant : (cosˆB)2+(sinˆB)2=1
Enfin, la tangente d’un angle peut être définie à partir du sinus et du cosinus de l’angle :
tanˆB=sinˆBcosˆB
Exemple :
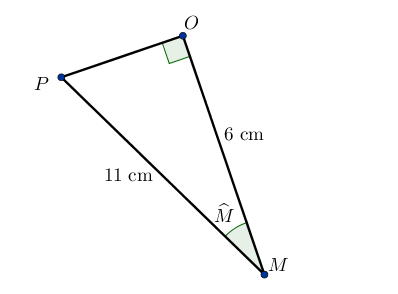
On cherche la valeur de l’angle ˆM.
Il s’agit donc de déterminer si il faut utiliser le cosinus, le sinus ou la tangente.
Ici, l’hypoténuse est donné ainsi que le côté adjacent : on utilise donc le cosinus.
Ainsi, cosˆM=MOMP
cosˆM=611≈0,545
Donc en utilisant la calculatrice pour déterminer l’angle en connaissant la valeur de son cosinus on trouve ˆM≈56,9°
Théorème de Pythagore
Théorème de Pythagore

Si ABC est un triangle rectangle en A, alors AB2+AC2=BC2
Ou encore :
la somme des carrés des deux petits côtés est égale au carré de l’hypoténuse.
Cette relation permet, en connaissant la longueur de deux côtés, de trouver la longueur du dernier côté.
Exemple :
Soit OMP un triangle rectangle en O, tel que OM=5 et MP=13.
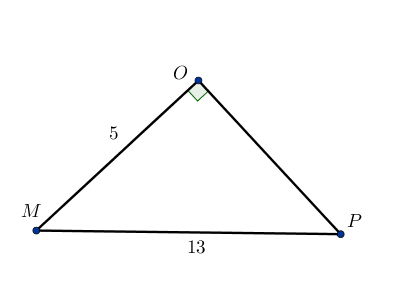
D’après le théorème de Pythagore appliqué au triangle rectangle OMP rectangle en O,
OM2+OP2=MP2
52+OP2=132
25+OP2=169
OP2=169–25
OP2=144
OP=√144
OP=12
