Annale – Graphes, suites

Vocabulaire sur les matrices

Vocabulaire sur les matrices

Définition

Une matrice $(n\times p)$ est un tableau à $n$ lignes et $p$ colonnes.

Exemple

$A=\begin{pmatrix} 3 & 4 & -1 \\ 0 & \dfrac{1}{2} & 7\\ \end{pmatrix}$    est une matrice $(2\times 3)$

Chaque nombre de $A$ est appelé coefficient: par exemple ${a}_{1;2}=4$ est le coefficient de la première ligne et de la deuxième colonne.

Vocabulaire

Matrice carrée: matrice ayant autant de lignes que de colonnes.

Matrice ligne: matrice ayant une ligne et plusieurs colonnes.

Matrice colonne: matrice ayant une colonne et plusieurs lignes.

Matrice unité:

$I_3=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix}$. 

$I_3$ est une matrice carrée de dimension $3$. Ses coefficients valent $1$ sur la diagonale principale et $0$ ailleurs.

Comment montrer qu'une suite est géométrique ?

Comment montrer qu’une suite est géométrique ?

Afin de montrer qu’une suite $(u_n)$ est géométrique, on commence par calculer les premiers termes en s’assurant qu’ils ne sont pas nuls puis on calcule les rapports des premiers termes : $\dfrac{u_1}{u_0}$ et $\dfrac{u_2}{u_1}$. 

Considérons par exemple la suite $u_n = 4 \times 3^n$. On a alors $\dfrac{u_1}{u_0} = 3$ et $\dfrac{u_2}{u_1} = 3$.

Si il apparait que le rapport des premiers termes est une constante $q$: on émet alors une conjecture en supposant que la constante ainsi trouvée est la raison de la suite. 

Il faut alors montrer en revenant à la définition d’une suite géométrique que $u_{n + 1} = q \times u_n$ pour tout $n \in \mathbb{N}$.

En revenant à notre exemple, on souhaite montrer que $u_{n + 1} = 3 u_n$.

Or :

$3 u_n = 3 \times ( 4 \times 3^n )$

$3 u_n= 4 \times 3^{n + 1}$

$3 u_n= u_{n + 1}$.

Donc $(u_n)$ est une suite géométrique de raison $3$ et de premier terme $u_0 = 4 \times 3^0 = 4 \times 1 = 4$.

Les graphes probabilistes

Les graphes probabilistes

Les graphes probabilistes permettent de transformer une étude probabiliste en un graphe et sa matrice.

Il existe des graphes d’ordre 2 ou d’ordre 3.

Les poids sur chaque arc correspondent à la probabilité de passer d’un événement à un autre en suivant le sens de parcours imposé par la flèche. 
La somme des probabilités inscrites sur les arcs partant d’un événement doit être égale à 1. 

Exemples : 

On considère le graphe d’ordre 3 suivant, et on le représente également par une matrice, contenant à l’intersection de la ligne $i$ avec la colonne $j$ la probabilité pour passer de l’événement $i$ à l’événement $j$.

En additionnant les probabilité d’une ligne, on vérifie que le résultat vaut 1. 

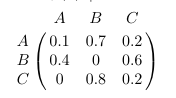
On peut aussi considérer un graphe d’ordre 2. 

$M = \left ( \begin{array}{cc} 0.3 & 0.7 \\ 0.8 & 0.2 \end{array} \right )$

Application :

On suppose que la situation que l’on étudie se traduit par le graphe d’ordre 2 précédent, que l’on peut traduire sous forme matricielle. 

On considère un état $P_0 = (a \ \; b)$ initial. Pour connaitre l’état $P_1$, on multiplie $P_0$ par $M$ et ainsi de suite. 

On trouve alors que pour tout $n \in \mathbb{N}, \ P_{n + 1} = P_n \times M$.

L’état $n + 1$ correspond à l’état $n$ multiplié par la matrice $M$.  

Il s’agit d’une suite géométrique de raison $M$ et de terme initial $P_0$. 

Ainsi, pour tout $n \in \mathbb{N}, P_n = P_0 \times M^n$. On veillera à ce que l’énoncé donne un premier terme pour $n = 0$. 

On essaie de savoir si en regardant pour des états $n$ lointains, le comportement de $P_n$ atteint un état stable, c’est à dire qu’il ne bouge plus, ou encore si la suite $(P_n)$ converge.

Or si aucun des 4 coefficients n’est égal à 0, il existe un état stable, que l’on appelle $P = (x \ \ y)$. 

Pour connaitre les valeurs de $x$ et $y$, on sait que la somme des probabilités vaut $1$ et comme il s’agit d’un état stable, il ne change pas lorsque on le multiplie pat la matrice $M$.

On obtient alors le système suivant : $\left \{ \begin{array}{c} PM = P \\ x + y = 1 \end{array} \right.$