Fonction paire-impaire - Traduction géométrique
Fonction paire/impaire – Traduction géométrique
I) Domaine de définition d’une fonction symétrique par rapport à $0$
On dit que le domaine de définition $\mathcal{D}$ d’une fonction est symétrique par rapport à $0$ si pour tout $x \in \mathcal{D}$, son opposé appartient aussi à $\mathcal{D}$, ou encore $-x \in \mathcal{D}$.
Exemple :
Soit $a > 0$, alors $[-a; a]$ est symétrique par rapport à $0$.
De même, $\mathbb{R}$ est symétrique par rapport à $0$.
II) Fonction paire et impaire
Définition : fonction paire
Une fonction $f$ définie sur un ensemble de définition $\mathcal{D}$ symétrique par rapport à $0$ est dite paire si pour tout $x \in \mathcal{D}$, $f(x) = f(-x)$.
Propriété :
Dans un repère orthogonal, la courbe représentative d’une fonction paire est symétrique par rapport à l’axe des ordonnées.
Exemple :
On s’intéresse à la fonction $x \mapsto x^2$.
Cette fonction est paire. En effet, pour tout réel $x$, $(-x)^2 = x^2$.
On trace donc la courbe représentative de la fonction carrée pour tout réel $x$ positif.
On considère un réel $x$ positif et on calcule son image par la fonction carrée.
Si on considère l’opposé de ce réel $x$, par définition de la parité de la fonction carré, $-x$ à la même image par cette fonction que $x$ : on a donc bien une symétrie par rapport à l’axe des ordonnées.

Il suffit donc d’étudier une fonction paire sur le domaine positif puis d’en déduire par symétrie la fonction sur le domaine négatif.
La parité permet donc de réduire le domaine d’étude d’une fonction.
Définition : Fonction impaire
Une fonction $f$ définie sur une ensemble de définition $\mathcal{D}$ symétrique par rapport à $0$ est dite impaire si pour tout $x \in \mathcal{D}$, $f(-x) = -f(x)$.
Propriété :
La courbe représentative d’une fonction impaire est symétrique par rapport à l’origine du repère $O$ : c’est une symétrie centrale.
Exemple :
On s’intéresse à la fonction $x \mapsto x^3$.
C’est une fonction impaire. En effet, pour tout réel $x$, $(-x)^3 = -x^3$ car le produit de trois réels négatifs est négatif.
Soit $x$ un réel positif, dont l’image par la fonction $f$ est $f(x)$.
L’image par cette même fonction de $-x$ est donc $-f(x)$.
Graphiquement, on remarque que cela correspond à une symétrie centrale par rapport à l’origine.

III) Exemple d’application
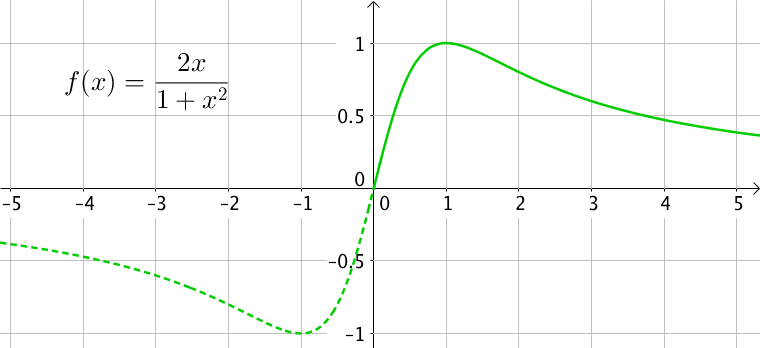
On cherche à étudier la parité de la fonction $f : x \mapsto \dfrac{2x}{1 + x^2}$ définie pour tout $x \in \mathbb{R}$.
Le domaine de définition de la fonction $f$ est symétrique par rapport à $0$.
Soit $x \in \mathbb{R}$, la méthode consiste à calculer $f(-x)$ puis de comparer le résultat à $f(x)$ :
$f(-x) = \dfrac{2 \times (-x)}{1 + (-x)^2} = \dfrac{-2x}{1 + x^2} = -\dfrac{2x}{1 + x^2} = -f(x)$
La fonction $f$ est donc impaire.
On peut donc réduire le domaine d’étude de la fonction $f$ aux réels positifs.