Médiane
Médiane d’une série statistique
Définition
La médiane correspond à la valeur pour laquelle la moitié des termes de la série statistique lui est inférieure et l’autre moitié supérieure.
Afin de calculer la médiane, il faut d’abord classer les termes de la série dans l’ordre croissant.
Exemple
Considérons par exemple la série statistique suivante :
65 ; 54 ; 84 ; 66 ; 84 ; 59 ; 70
que l’on réordonne par ordre croissant
54 ; 59 ; 65 ; 66 ; 70 ; 84 ; 84
Ici le nombre médian est 66 : il y a trois termes plus petits et trois termes plus grands.
Lorsque la série statistique contient un nombre impair de termes (N), la médiane appartient à la série statistique et est le terme de rang N+12.
Autre exemple
Si on considère maintenant la série suivante composé de 8 termes :
65 ; 54 ; 84 ; 66 ; 84 ; 59 ; 70 ; 72
qui donne une fois classée par ordre croissant :
54 ; 59 ; 65 ; 66 ; 70 ; 72 ; 84 ; 84.
D’après la définition, il doit y avoir quatre termes plus petits que la médiane et quatre termes plus grands : la médiane se situe donc entre 66 et 70.
Pour trouver la médiane dans ce cas-là, il faut prendre le terme le plus grand de la série inférieure et le terme le plus petit de la série supérieure et faire leur moyenne.
Ainsi, si la série statistique contient un nombre pair de termes (N), alors la médiane est la moyenne du terme de rang N2 et de rang N2+1.
Ainsi, la médiane dans ce cas là est égale à 66+702=68.
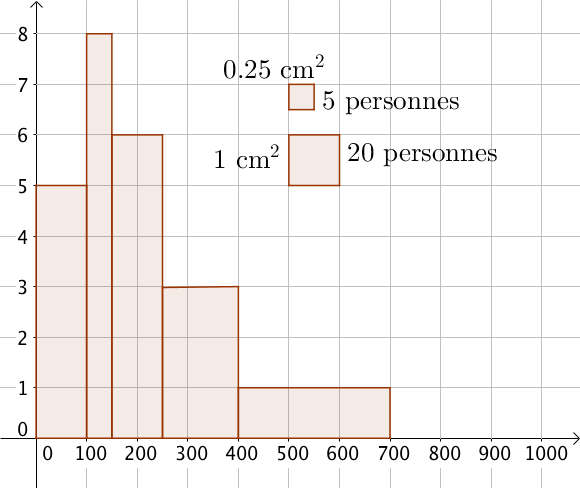
Histogramme à largeur variable
Histogramme à largeur variable
Dans certains cas, les histogrammes sont à largeur variable, car la série statistique que l’on étudie est regroupée en classes de largeur variable.
Considérons l’exemple suivant de la distribution de l’argent de poche au sein d’un groupe d’étudiant que l’on regroupe par classe de longueurs inégales.
| classe | [0;100[ | [100;150[ | [150;250[ | [250;400[ | [400;700[ |
| Effectif | 100 | 80 | 120 | 90 | 60 |
Dans un histogramme, il faut que l’aire des rectangles soit proportionnelle à l’effectif.
Ici, 1cm en abscisse représente 100 personnes et 1cm2 pour un effectif de 20 personnes. Si on coupe en 4 carrés égaux un carré de 1 cm2, on obtient alors un effectif de 5 personnes.
Afin de connaitre la longueur L du rectangle, on utilise la formule de l’aire A:
A=L×l, ou encore L=Al, avec l qui correspond à la largeur de l’intervalle (exprimée en centaines dans notre exemple) et donc la largeur du rectangle.
On regarde le premier rectangle. On souhaite qu’il représente une population de 100 personnes et on cherche tout d’abord son aire A. Or 20 personnes sont représentées par une aire de 1 cm2.
On utilise donc le tableau de proportionnalité suivant :
| Effectif | 20 | 100 |
| Aire (cm2) | 1 | A |
On trouve alors que A=10020=5 cm2.
Pour trouver la hauteur L, on utilise la formule rappelée précédemment :
L=Al=51=5.
On peut de même effectuer les calculs pour les autres classes, et on obtient alors l’histogramme suivant :